Archimedes, Issac Newton, and Albert Einstein Compared: Titans of Physics
Absolutely! Archimedes, Isaac Newton, and Albert Einstein are undoubtedly physics and scientific thought giants. Let’s break down their areas of expertise and major contributions:
Archimedes (c. 287 – c. 212 BC)
- Field: Ancient Greek mathematician, physicist, and engineer.
- Focus: Mechanics, hydrostatics, mathematics
- Major Discoveries:
- Archimedes Principle: The science behind buoyancy (an object immersed in fluid experiences an upward force equal to the weight of the fluid displaced).
- The Lever: Explained the principles behind levers and their mechanical advantage.
- Archimedes Screw: An early water pump.
- Infinitesimals: Methods closely resembling integral calculus
- Legacy: Archimedes is considered one of the greatest mathematicians of antiquity, laying the foundations for engineering principles and calculus.
Isaac Newton (1643 – 1727)
- Field: English mathematician, physicist, astronomer
- Focus: Classical mechanics, optics, calculus
- Major Discoveries:
- Laws of Motion: The three fundamental laws governing how objects move in response to forces.
- Universal Gravitation: Every object in the universe attracts another object with a predictable force.
- Calculus: Revolutionized mathematics, essential for scientific analysis.
- Optics: Discovered light is made of a spectrum of colors, and the first reflecting telescope was built.
- Legacy: Newton is largely considered the founder of classical physics and one of the most influential scientists of all time.
Albert Einstein (1879 – 1955)
- Field: German-born theoretical physicist
- Focus: Relativity, quantum mechanics
- Major Discoveries:
- Special Relativity: Revolutionized understanding of space and time, introduced the famous E=mc² equation (energy-mass equivalence).
- General Relativity: Redefined gravity as a curvature of spacetime.
- Photoelectric Effect: Explained how light interacts with matter, a key foundation of quantum mechanics.
- Brownian Motion: Provided evidence for the existence of atoms.
- Legacy: Einstein reshaped our understanding of the universe, heavily influencing modern physics and cosmology.
Comparison
- Shifting Paradigms: Each of these titans challenged and overthrew the scientific understanding of their day. Archimedes established fundamental mechanics; Newton systematized it and expanded knowledge to cosmic scales; Einstein shattered concepts of space, time, and gravity.
- The breadth of Impact: Archimedes was primarily a mathematician and engineer. Newton’s work was fundamental to multiple fields. Einstein revolutionized our entire conception of the physical universe.
- Building on the Past: These figures built upon one another’s work, even with centuries separating them. Newton refined the understanding of motion that Archimedes had pioneered. Einstein’s breakthroughs relied on the mathematical language and tools refined by those who came before.
Let me know if you’d like more details on a specific scientist or a deeper dive into their discoveries!
AI Archimedes History
Archimedes (Wiki Image).
-
“Give me a lever long enough and a fulcrum on which to place it, and I shall move the world.” – This is his most famous statement, illustrating the power of levers and the principles of mechanics.
-
“Eureka!” (I have found it!) – This exclamation, supposedly uttered as he discovered a method for determining the purity of gold, has become synonymous with moments of scientific discovery.
-
“The shortest distance between two points is a straight line.” – A simple but fundamental geometric principle attributed to Archimedes.
-
“Mathematics reveals its secrets only to those who approach it with pure love, for its own beauty.” – This expresses his passion for mathematics as a pursuit worthy in its own right.
-
“Give me but a firm spot on which to stand, and I shall move the earth.” – A variation on the lever quote showcasing his confidence in the principles of mechanics.
-
“Those who claim to discover everything but produce no proofs of the same may be confused as having actually pretended to discover the impossible.” – A critique of those who boast of discoveries without providing evidence.
-
“Don’t disturb my circles!” – Allegedly said to a Roman soldier who interrupted his mathematical work, highlighting his dedication to his craft.
-
“Man has always learned from the past. The present is the result of the past, and the future will be the result of the present.” – This reflects his awareness of the interconnectedness of knowledge and the importance of building upon past discoveries.
-
“There are things which seem incredible to most men who have not studied Mathematics.” – A testament to his belief in the power of mathematics to unlock mysteries and explain the world.
-
“Numbers rule the universe.” – This reflects the Pythagorean influence on his thinking, emphasizing the fundamental role of mathematics in understanding the cosmos.
| Life Stage | Approximate Year | Contribution to Physics | Significance |
|---|---|---|---|
| Early Career | 260s – 250s BC | Law of the Lever: Formulated the mathematical principles of levers, explaining how they work and their relationship between force, load, and fulcrum. | This laid the foundation for understanding mechanical advantage and revolutionized engineering and construction. |
| Center of Gravity: Developed the concept of the center of gravity and its importance in the equilibrium of objects. | This concept is fundamental to understanding stability and balance in structures and is still used in physics and engineering today. | ||
| Mid-Career | 250s – 240s BC | Hydrostatics: Laid the groundwork for the field of hydrostatics, investigating the behavior of fluids at rest. | This led to his famous discovery of the principle of buoyancy, known as Archimedes’ Principle. |
| Archimedes’ Principle: Discovered that the buoyant force on an object submerged in a fluid is equal to the weight of the fluid displaced by the object. | This principle revolutionized our understanding of buoyancy and has countless applications in shipbuilding, engineering, and fluid mechanics. | ||
| Later Career | 240s – 212 BC | Optics: Conducted research on the properties of light, including reflection and refraction. | While much of his work in this area is lost, he is believed to have made significant contributions to the understanding of optics. |
| Astronomy: Built astronomical instruments and made observations of the heavens. | He is credited with constructing a planetarium that could demonstrate the movements of the sun, moon, and planets. |
Archimedes: The Greatest Mind in Ancient History
(YouTube video)
Archimedes (c. 287 – c. 212 BC) was a Greek mathematician, physicist, astronomer, engineer, inventor, and weapon designer from the ancient Greek city of Syracuse, Sicily. Although his fame rests on his inventions, Archimedes is widely considered one of the greatest mathematicians of all time, and some of his inventions, such as the Archimedes screw, are still in use today.
Early life and education
Archimedes was born in Syracuse in c. 287 BC. He was the son of Phidias, an astronomer, and may have been related to Hiero II, the king of Syracuse. According to Plutarch, Archimedes was sent to Alexandria, Egypt, to study mathematics and astronomy. This environment gave Archimedes access to knowledge and the works of earlier mathematicians, such as Euclid and Eratosthenes.
Mathematical discoveries
Archimedes made significant contributions to mathematics, including:
- The method of exhaustion: A technique for approximating the areas and volumes of curves and solids.
- The principle of buoyancy: An object immersed in a fluid experiences an upward buoyant force equal to the weight of the liquid it displaces.
- The discovery of the formula for the volume of a sphere: The formula for the volume of a sphere is (4/3)πr^3, where π is the ratio of the circumference of a circle to its diameter and r is the sphere’s radius.
- The discovery of the formula for the surface area of a sphere: The formula for the surface area of a sphere is 4πr^2.
Inventions
Archimedes was also a prolific inventor. His inventions include:
- The Archimedes screw: A device used to raise water from a lower level to a higher level.
- The compound pulley: A system of pulleys that can lift cumbersome objects.
- The hydraulic screw: A device used to transport water over long distances.
- The burning mirror: A device used to focus sunlight on enemy ships, causing them to catch fire.
- The celestial sphere: This device represents the positions of the stars and planets in the sky.
Death of Archimedes
Archimedes was killed during the Second Punic War when Syracuse was captured by the Romans in 212 BC. According to Plutarch, Archimedes worked on a mathematical problem when the Romans stormed the city. A Roman soldier approached Archimedes and told him to come and meet the Roman general, Marcus Claudius Marcellus. Archimedes refused to leave his work until he had finished it, so the soldier killed him.
Legacy
Archimedes is considered one of the greatest mathematicians of all time. His inventions profoundly impacted the development of science and technology, and his mathematical discoveries continue to be studied today.
Archimedes’ Early Life and Education
While Archimedes studied in Alexandria and was familiar with their work, Euclid and Conon lived about a century before him.
-
Euclid: A Greek mathematician known as the “father of geometry.” His most famous work, “Elements,” laid the foundation for geometry for centuries.
-
Conon of Samos: A Greek astronomer and mathematician known for his work on conic sections and contributions to astronomy.
It’s more likely that Archimedes learned from their writings and works, as well as those of other scholars in Alexandria, rather than receiving direct instruction. However, he corresponded with and exchanged ideas with other mathematicians of his time, including Conon’s pupil, Dositheus of Pelusium.
Archimedes’ time in Alexandria was pivotal in his development as a mathematician and scientist. It exposed him to a wealth of knowledge and expertise, which undoubtedly influenced his groundbreaking work in mathematics, physics, engineering, and astronomy.
The method of exhaustion: A technique for approximating the areas and volumes of curves and solids.
The method of exhaustion is a pre-calculus technique used to approximate the areas and volumes of irregular shapes by inscribing or circumscribing them with increasingly accurate polygons or polyhedra. Ancient Greek mathematicians like Eudoxus of Cnidus and Archimedes developed this method, which laid the groundwork for integral calculus.
Key Principles:
- Inscribe or Circumscribe: The method involves either inscribing (fitting inside) or circumscribing (fitting around) the target shape with simpler shapes (like polygons for areas or polyhedra for volumes) whose areas or volumes can be easily calculated.
- Increase Complexity: The inscribed or circumscribed shapes are progressively refined by increasing the number of sides (for polygons) or faces (for polyhedra), making them more closely approximate the target shape.
- Limit: As the number of sides or faces approaches infinity, the areas or volumes of the approximating shapes converge to the true area or volume of the original irregular shape.
Example: Approximating the Area of a Circle
- Inscribe a square within a circle.
- Inscribe a regular octagon within the circle, its vertices touching the midpoint of each side of the square.
- Continue inscribing polygons with more and more sides (hexadecagon, 32-gon, etc.).
- As the number of sides increases, the polygon’s area approaches the circle’s area.
Significance:
- Foundation for Calculus: The method of exhaustion foreshadowed the development of integral calculus, which provides a rigorous and systematic way to calculate areas and volumes using limits and infinitesimals.
- Historical Importance: It was a significant mathematical achievement in ancient times, demonstrating the power of approximating complex problems with simpler ones and illustrating the concept of limits.
Limitations:
- Tedious: The method can be computationally intensive, requiring calculating areas or volumes for increasingly complex shapes.
- Approximation: It provides an approximation rather than an exact solution, although the accuracy can be improved by increasing the complexity of the approximating shapes.
Let me know if you have any other questions about the method of exhaustion.
An object immersed in a fluid experiences an upward buoyant force equal to the weight of the fluid it displaces.
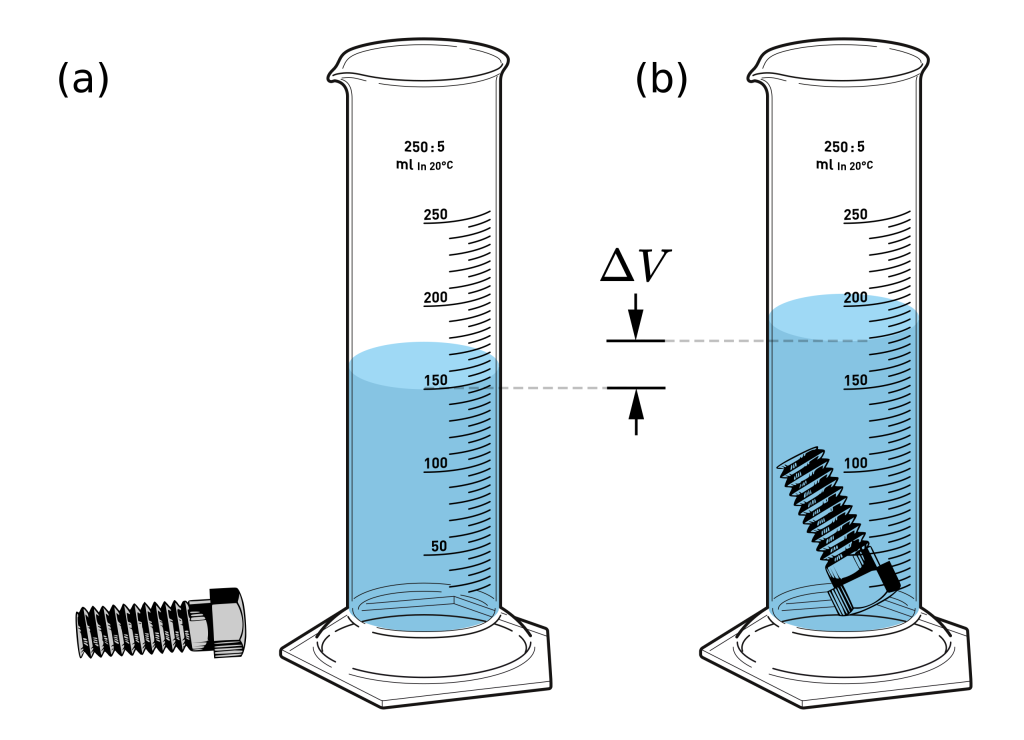Volume measurement by displacement, (a) before and (b) after an object has been submerged. The amount by which the liquid rises in the cylinder (∆V) is equal to the object’s volume (Wiki Image).
Archimedes’ principle, a fundamental concept in fluid mechanics, states that an object immersed in a fluid experiences an upward buoyant force equal to the weight of the fluid it displaces. The Greek mathematician and inventor Archimedes discovered this principle in the 3rd century BC.
The buoyant force arises from the pressure difference between the fluid below and above the immersed object. Due to the weight of the overlying fluid, the pressure at the bottom of the object is greater than the pressure at the top. This pressure difference creates an upward force on the object, counteracting the downward force of gravity.
The buoyant force is directly proportional to the fluid’s density, the volume of the fluid displaced, and the acceleration due to gravity. This means the buoyant force is greater for denser fluids and larger objects.
Archimedes’ principle has several critical applications, including
- Ship design: Archimedes’ principle is essential for designing ships and submarines to ensure they are buoyant and can float in water.
- Hot air balloons: The buoyant force of air is harnessed in hot air balloons to lift them into the sky.
- Hydrometers: Hydrometers use the principle of buoyancy to measure the density of fluids.
- Swimming: The buoyant force of water helps swimmers stay afloat and control their movements in the water.
Archimedes’ principle is a fundamental concept in physics and fluid mechanics. It has profoundly impacted our understanding of fluids and their interactions with objects. It continues to be applied in various fields, from engineering and design to sports and science.
Archimedes’ investigation of the celestial sphere: This device represents the positions of the stars and planets in the sky.
Archimedes’ celestial sphere was an early example of a planetarium, a mechanical model designed to represent the positions and movements of stars and planets as seen from Earth. It is considered a marvel of ancient Greek engineering and ingenuity.
The device is said to have consisted of a hollow sphere with rings representing the celestial equator, the ecliptic (the Sun’s apparent path), and the zodiac constellations. The planets were likely represented by small spheres or markers that moved along their respective paths.
While no physical remains of Archimedes’ celestial sphere have been found, its existence and functionality are attested by several ancient sources, including Cicero, Ovid, and Pappus of Alexandria. They describe how the sphere could simulate the daily rotation of the sky, the moon’s monthly phases, and the planets’ annual movements, including retrograde motion.
Archimedes’ celestial sphere served as a tool for astronomical observation and calculation and as a demonstration of the cosmos’ intricate workings. It reflected the advanced state of Greek astronomy and mechanics during the Hellenistic period. The sphere is also a testament to Archimedes’ remarkable intellect and ability to translate complex astronomical theories into tangible, mechanical models.
Archimedes Siege of Syracuse
The Siege of Syracuse was a pivotal event in the Second Punic War between Rome and Carthage, lasting from 214 to 212 BC. The city of Syracuse, located on the eastern coast of Sicily, was a major Greek stronghold and a key target for the Romans. The siege was notable for the innovative defensive strategies employed by Archimedes, a renowned mathematician and engineer who served as an advisor to the Syracusan forces.
Archimedes’ Defensive Innovations
Archimedes is credited with developing several ingenious devices that helped repel Roman attacks during the siege. These included:
-
- The Claw: A long, crane-like device with a grappling hook that could snatch Roman ships from the sea and lift them onto land, where they were easily overturned and destroyed.
-
- The Burning Mirrors: A series of highly polished mirrors that could concentrate sunlight and set fire to Roman ships as they approached the city walls.
-
- Catapults: Large-scale catapults that could hurl massive stones and projectiles at the Roman ships and troops, inflicting significant damage.
According to Plutarch:
“A ship was frequently lifted to a great height [by the Claw] in the air (a dreadful thing to behold) and was rolled to and fro, and kept swinging until the mariners were throw out when at length it was dashed the rocks, or let fall. At the engine that [Proconsul] Marcellus brought upon the bridge of the ship, called a Sambuca, from some resemblance it had to an instrument of music, while it was yet approaching the wall, there was discharged a piece of rock of ten talents weight [710 pounds] than a second and a third, which, striking upon it with immense force and a noise like thunder, broke all its foundation to pieces, shook out all its fastings, and completely dislodged it from the bridge.”
The Fall of Syracuse
Despite Archimedes’ ingenious defenses, the Romans eventually captured Syracuse after a prolonged siege. They exploited a weakness in the city’s defenses, gaining access to a wall section left unguarded due to a festival. The Romans then poured into the city, overcoming the Syracusan forces.
Archimedes’ death during the sack of Syracuse is a poignant reminder of the brutality of warfare in the ancient world. Despite his contributions to the defense of Syracuse, he was reportedly killed by a Roman soldier who did not recognize him.
Archimedes’ Legacy
Archimedes’ legacy extends far beyond the Siege of Syracuse. He is considered one of the greatest mathematicians and scientists of all time, making significant contributions to geometry, physics, astronomy, and engineering. His inventions, such as the Archimedes screw, have had a lasting impact on technology and continue to be studied and admired today.
The Siege of Syracuse is a testament to Archimedes’ ingenuity and resourcefulness in the face of overwhelming odds. His defensive innovations prolonged the siege and inflicted heavy losses on the Romans, demonstrating the power of scientific knowledge in warfare.
AI Issac Newton History
Issac Newton (Wiki Image).
-
“If I have seen further, it is by standing on the shoulders of Giants.” – This humble acknowledgment recognizes the contributions of those who came before him in advancing scientific knowledge.
-
“Truth is ever to be found in simplicity, and not in the multiplicity and confusion of things.” – This reflects his belief in seeking elegant, fundamental principles to explain the complexities of the natural world.
-
“To every action, there is always opposed an equal reaction.” – Newton’s Third Law of Motion, summarizing the fundamental principle of how forces interact.
-
“I do not know what I may appear to the world, but to myself, I seem to have been only like a boy playing on the sea-shore and diverting myself in now and then finding a smoother pebble or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me.” – This humble statement reveals his sense of awe and wonders at the vastness of knowledge yet to be explored.
-
“We build too many walls and not enough bridges.” – A commentary on the importance of communication, collaboration, and understanding between individuals and nations.
-
“Plato is my friend – Aristotle is my friend – but my greatest friend is truth.” – Expressing his dedication to pursuing truth above all else, even the opinions of respected figures.
-
“I can calculate the motion of heavenly bodies, but not the madness of people.” – This highlights the unpredictability of human behavior compared to the laws governing the natural world.
-
“Tact is the knack of making a point without making an enemy.” – A reminder of the importance of diplomacy and tactful communication.
-
“If I have done the public any service, it is due to my patient thought.” – Emphasizing the value of persistent, focused thinking in achieving success and making significant contributions.
-
“What we know is a drop, what we don’t know is an ocean.” – A humble acknowledgment of the vastness of knowledge and the limits of human understanding.
| Year | Age | Contribution to Physics | Significance |
|---|---|---|---|
| 1665-1667 | 22-24 | Early work on calculus: He independently developed a form of calculus, which he called “fluxions,” providing a new mathematical framework for understanding change and motion. | While not published until much later, this was foundational for his later work in physics and is a cornerstone of modern mathematics. |
| 1666 | 23 | Experiments with prisms and light: Conducted groundbreaking experiments with prisms, demonstrating that white light comprises a spectrum of colors. | This overturned centuries of belief about the nature of light and laid the foundation for modern optics. |
| 1660s – 1670s | 20s | Laws of Motion: He developed his three laws of motion, describing the relationship between a body and the forces acting upon it. | These laws form the basis of classical mechanics and are still fundamental to our understanding of motion and forces. |
| 1687 | 44 | Publication of Principia Mathematica: His masterpiece, Philosophiæ Naturalis Principia Mathematica, outlined his laws of motion and the law of universal gravitation. | This work revolutionized physics, providing a unified framework for understanding the motion of objects on Earth and in the heavens. |
| 1690s | 50s | Further work on optics: He continued his work on optics, studying the properties of light and developing a theory of color. | He invented the reflecting telescope, which significantly improved astronomical observation. |
Sir Isaac Newton: Unhappy Scientific Genius | Full …
(YouTube video)
Isaac Newton was an English mathematician, physicist, astronomer, alchemist, theologian, and author widely recognized as one of the most influential scientists of all time and a key figure in the Scientific Revolution. His book Philosophiæ Naturalis Principia Mathematica (“Mathematical Principles of Natural Philosophy”), first published in 1687, laid the foundations of classical mechanics. Newton also made seminal contributions to optics and shares credit with Gottfried Wilhelm Leibniz for the development of calculus.
Early Life and Education
Isaac Newton was born on December 25, 1642 (January 4, 1643, New Style) in Woolsthorpe Manor, Woolsthorpe-by-Colsterworth, a hamlet in Lincolnshire, England. His father, Isaac Newton, died three months before he was born. His mother, Hannah Ayscough, remarried after his father’s death and left him in the care of his grandmother.
Newton showed an early aptitude for mechanics and mathematics. He attended King’s School in Grantham, where he excelled in his studies. In 1661, he entered Trinity College, Cambridge, where he studied mathematics and natural philosophy.
Scientific Discoveries
During his time at Cambridge, Newton made several groundbreaking discoveries in mathematics and physics. He developed calculus, now considered an essential tool for scientists and engineers. He also formulated the three laws of motion, which describe the behavior of objects in motion. Newton’s laws of motion laid the foundation for classical mechanics, the branch of physics that deals with the motion of objects.
In addition to his work in mathematics and physics, Newton made significant contributions to optics. He discovered that white light comprised a spectrum of colors and developed a reflecting telescope, now known as the Newtonian telescope.
Later Life and Legacy
After graduating from Cambridge in 1665, Newton returned to Woolsthorpe Manor during the Great Plague of London. During this period, he made many of his most important discoveries. In 1667, he returned to Cambridge and was appointed Lucasian Professor of Mathematics. He held this position for over 30 years.
In 1687, Newton published his most famous work, Philosophiæ Naturalis Principia Mathematica. This book laid the foundations of classical mechanics and established Newton as one of the most important scientists ever.
Newton was elected President of the Royal Society in 1705 and was knighted by Queen Anne in 1705. He died in London on March 31, 1727, and was buried in Westminster Abbey.
Newton’s work has had a profound impact on science and technology. His laws of motion and his theory of gravity are still used today to understand the motion of planets and stars. His work in optics has led to the development of telescopes and microscopes. His work in mathematics has led to the development of calculus, which is now used in various fields.
Newton is considered one of the greatest scientists of all time. His work has profoundly impacted our understanding of the universe and led to the development of many important technologies.
Newton and Leibniz of Calculus.
Isaac Newton and Gottfried Wilhelm Leibniz are widely recognized as the co-founders of calculus, a branch of mathematics that deals with the rates of change and accumulations of quantities. Both independently developed the fundamental concepts of calculus, including differentiation and integration, during the late 17th century.
Isaac Newton’s Contributions to Calculus
His interest in physics and astronomy primarily drove Newton’s work on calculus. He developed calculus to solve problems in these fields, such as understanding planets’ motion and fluids’ behavior. Newton’s calculus, which he called “fluxions,” was based on the idea of infinitesimals, which are infinitely small quantities. He used fluxions to represent rates of change and to solve differential equations.
Gottfried Wilhelm Leibniz’s Contributions to Calculus
Leibniz’s development of calculus was motivated by his desire to create a more rigorous and systematic approach to mathematics. He developed calculus independently of Newton, and his notation is the one that is still used today. Leibniz’s calculus, which he called “differential calculus,” was based on the idea of differentials, which are small differences between variables. He used differentials to represent rates of change and to find antiderivatives.
The Controversy over Calculus
Despite their independent development, Newton and Leibniz became embroiled in a bitter dispute over who should be credited with inventing calculus. Newton’s supporters claimed that he had developed calculus earlier than Leibniz, while Leibniz’s supporters argued that his notation was more elegant and easier to use. The controversy ultimately damaged both men’s reputations and delayed the widespread adoption of calculus.
Reconciliation and Legacy
Despite the controversy, Newton and Leibniz’s contributions to calculus are undeniable. Their work laid the foundation for modern mathematics and physics, which continues to be used in various fields today.
Here is a table summarizing the key differences between Newton’s and Leibniz’s approaches to calculus:
| Feature | Newton’s Calculus (Fluxions) | Leibniz’s Calculus (Differential Calculus) |
| Notation | Uses dots above variables to represent derivatives | Uses dy/dx to represent derivatives |
| Concept of change | Based on infinitesimals | Based on differentials |
| Focus | Applications in physics and astronomy | Mathematical rigor and elegance |
drive_spreadsheetExport to Sheets
Despite these differences, Newton’s and Leibniz’s methods are equivalent and can solve the same problems. Their work has profoundly impacted mathematics and science, and it continues to be essential for understanding the world around us.
Newton made significant contributions to optics.
Yes, Isaac Newton made significant contributions to optics, including:
-
Discovery of the composition of white light: Newton conducted experiments with prisms and discovered that white light is composed of a spectrum of colors. This discovery led to the development of new types of telescopes and microscopes.
-
Development of the reflecting telescope: Newton was dissatisfied with the performance of refracting telescopes, which suffered from chromatic aberration. To eliminate this problem, he developed a reflecting telescope, which uses mirrors instead of lenses. The reflecting telescope is still widely used today.
-
Formulation of the laws of light: Newton formulated the laws of reflection and refraction, which describe how light bends when it interacts with surfaces. These laws are still used today to design optical instruments.
-
Discovery of the polarization of light: Newton discovered that light can be polarized, which means that its electric field can vibrate in a single direction. This discovery led to the development of new types of optical instruments, such as polarizing filters.
Newton’s contributions to optics have profoundly impacted our understanding of light and its interaction with matter. His work has led to developing many important technologies, including telescopes, microscopes, and lasers.
Newton’s laws of motion laid the foundation for classical mechanics, the branch of physics that deals with object motion.
Sir Isaac Newton’s three laws of motion are fundamental principles that describe the relationship between the force acting on an object and its resulting motion. These laws have been instrumental in shaping our understanding of classical mechanics, the branch of physics that deals with the motion of objects and the forces that act upon them.
First Law of Motion: The Law of Inertia
Newton’s first law of motion, also known as the law of inertia, states that an object at rest will remain at rest, and an object in motion will continue with a constant velocity unless acted upon by an external force. This means that an object will maintain its state of motion (stationary or moving at a constant speed) unless a force is exerted upon it to change that state.
Second Law of Motion: The Law of Acceleration
Newton’s second law of motion, also known as the law of acceleration, establishes the relationship between the force acting on an object, its mass, and its resulting acceleration. The law states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. This means that the stronger the force applied to an object, the greater its acceleration, while a heavier object will experience a smaller acceleration for the same applied force.
Third Law of Motion: The Law of Action and Reaction
Newton’s third law of motion, also known as the law of action and reaction, states an equal and opposite reaction for every action. This means that when an object exerts a force on another object, the second object simultaneously exerts a force back on the first object. These forces are equal in magnitude and opposite in direction.
The three laws of motion form the foundation of classical mechanics and profoundly impact our understanding of the physical world. They have been applied to explain various phenomena, from planets’ motion to everyday objects’ behavior. Newton’s laws continue to be essential tools for scientists and engineers in their studies of motion and mechanics.
Newton Gravitation
A wood engraving of Newton’s famous steps under the apple tree (Wiki Image).
Sir Isaac Newton’s law of universal gravitation is a fundamental principle in physics that describes the attractive force between all objects with mass. It states that every particle attracts every other particle in the universe with a force directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers.
The law can be expressed mathematically as:
F = G * (m1 * m2) / r^2
Where:
- F is the gravitational force between the two particles
- G is the universal gravitational constant, approximately 6.674 × 10^-11 N m²/kg²
- m1 and m2 are the masses of the two particles
- r is the distance between the centers of the two particles
The law of universal gravitation has profoundly impacted our understanding of the universe. It has been used to explain a wide range of phenomena, from the motion of planets and stars to the tides on Earth. It is one of the most important laws in physics and continues to be essential for scientists and engineers in their studies of gravity and the cosmos.
Here are some examples of how Newton’s law of universal gravitation has been applied to explain natural phenomena:
- The motion of planets: Newton’s law of universal gravitation explained why planets orbit the Sun in elliptical paths. He showed that the force of gravity between the Sun and a planet is responsible for keeping the planet in its orbit.
- The tides on Earth: Newton’s law of universal gravitation explains why the Earth experiences two tides per day. He showed that the gravitational pull of the Moon and Sun on the Earth’s oceans creates the tides.
- The formation of stars and galaxies: Newton’s law of universal gravitation explains how stars and galaxies form from collapsing clouds of gas and dust. The gravitational pull of the particles in the cloud causes the cloud to collapse and eventually form a star or a galaxy.
Newton’s law of universal gravitation is a powerful tool for understanding the universe. It has been used to make many important predictions about the behavior of objects in space. It has helped us to develop a deeper understanding of the forces that govern the cosmos.
AI Albert Einstein History
Albert Einstein (Wiki Image).
-
“Imagination is more important than knowledge. Knowledge is limited. Imagination encircles the world.”
-
“Two things are infinite: the universe and human stupidity, and I’m not sure about the universe.”
-
“If you can’t explain it to a six-year-old, you don’t understand it yourself.”
-
“The difference between genius and stupidity is that genius has its limits.”
-
“Life is like riding a bicycle. To keep your balance, you must keep moving.”
-
“Logic will get you from A to Z; imagination will get you everywhere.”
-
“Anyone who has never made a mistake has never tried anything new.”
-
“The only source of knowledge is experience.”
-
“A person who never made a mistake never tried anything new.”
-
“The most beautiful thing we can experience is the mysterious. It is the source of all true art and science.”
-
“The world as we have created it is a process of our thinking. It cannot be changed without changing our thinking.”
-
“The true sign of intelligence is not knowledge but imagination.”
-
“The only thing that interferes with my learning is my education.”
-
“The most important thing is to not stop questioning. Curiosity has its own reason for existing.”
-
“We cannot solve our problems with the same thinking we used when we created them.”
| Year | Age | Contribution to Physics | Significance |
|---|---|---|---|
| 1905 | 26 | Photoelectric Effect: Published a paper explaining the photoelectric effect, proposing that light consists of discrete packets of energy called photons. | This work laid the foundation for quantum theory and earned him the Nobel Prize in Physics in 1921. |
| 1905 | 26 | Brownian Motion: Explained Brownian motion (the random movement of particles suspended in a fluid) as evidence for the existence of atoms and molecules. | This provided crucial support for the atomic theory of matter. |
| 1905 | 26 | Special Relativity: He published his theory of special relativity, which revolutionized our understanding of space, time, and motion. | This theory introduced the concept that time and space are relative and interconnected and that the speed of light is constant for all observers. |
| 1905 | 26 | Mass-Energy Equivalence: Derived the famous equation E=mc², which expresses the equivalence of mass and energy. | This equation has profound implications for our understanding of the universe and is fundamental to nuclear physics. |
| 1915 | 36 | General Relativity: Published his theory of general relativity, which describes gravity as a curvature of spacetime caused by mass and energy. | This theory revolutionized our understanding of gravity and has significant implications for cosmology and astrophysics. |
| 1917 | 38 | Cosmological Constant: Introduced the cosmological constant into his equations of general relativity to account for a static universe. | While later retracted, this concept has been revived in modern cosmology to explain the universe’s accelerating expansion. |
| 1920s-1930s | 40s-50s | Unified Field Theory: Worked on a unified field theory to combine gravity and electromagnetism into a single framework. | Although unsuccessful, this pursuit influenced later attempts at unification in theoretical physics. |
The Secret Life of Albert Einstein
(YouTube video)
Albert Einstein was a German-born theoretical physicist who developed the theory of relativity, one of the two pillars of modern physics (alongside quantum mechanics). His work is also known for its influence on the philosophy of science.
Early Life and Education
Albert Einstein was born on March 14, 1879, in Ulm, in the Kingdom of Württemberg in the German Empire. His father was Hermann Einstein, a salesman and engineer. His mother was Pauline Koch. Einstein had a younger sister named Maria.
Einstein’s family moved to Munich in 1880. From 1888 to 1894, he attended the Luitpold Gymnasium, a Catholic school. He was not a good student and often skipped class, but he was interested in mathematics and physics.
In 1895, Einstein moved to Switzerland to attend the Swiss Federal Institute of Technology in Zurich. He graduated in 1900 with a degree in physics.
Career
After graduating from college, Einstein worked as a patent clerk in Bern, Switzerland. He continued to study physics in his spare time. In 1905, he published four groundbreaking papers in the Annalen der Physik, a German physics journal. These papers became known as the “Annus Mirabilis” papers (Latin for “miracle year”).
The first paper introduced the special theory of relativity, which showed that the speed of light is constant in all inertial frames of reference. The second paper introduced the photoelectric effect, which showed that light comprises particles called photons. The third paper introduced Brownian motion, which showed that atoms and molecules are real and that they are constantly moving. The fourth paper introduced the mass–energy equivalence formula, which is expressed as E = mc², where E is energy, m is mass, and c is the speed of light.
Einstein’s work on relativity revolutionized our understanding of space, time, and gravity. His work on the photoelectric effect laid the foundation for quantum mechanics. His work on Brownian motion provided further evidence for the existence of atoms and molecules. His work on mass–energy equivalence showed that mass and energy are equivalent.
Einstein’s work earned him the Nobel Prize in Physics in 1921. He was awarded the prize “for his services to theoretical physics, especially for his discovery of the law of the photoelectric effect.”
Later Life
Einstein moved to the United States in 1933 to escape the rise of Nazism in Germany. He became a professor at the Institute for Advanced Study in Princeton, New Jersey. He continued to work on physics and philosophy until he died in 1955.
Legacy
Albert Einstein is considered one of the most influential scientists ever. His work has had a profound impact on our understanding of the universe. He is also known for his pacifist views and commitment to social justice.
Here are some of Einstein’s most famous quotes:
- “Imagination is more important than knowledge. For knowledge is limited, whereas imagination embraces the entire world, stimulating progress, giving birth to inventions.”
- “Never give up on what you really want to do. The person with big dreams is more powerful than one with all the facts.”
- “The important thing is not to stop questioning. Curiosity has its own reason for existence.”
- “The world is a dangerous place to live, not because of the evil people, but because of the people who don’t do anything about it.”
- “We cannot solve our problems with the same thinking we used when creating them.”
Albert Einstein’s legacy continues to inspire and inform people around the world. He is a reminder of the power of imagination, curiosity, and perseverance.
That the speed of light is constant in all inertial frames of reference.
That is correct! It is one of the fundamental postulates of Einstein’s theory of special relativity.
The Speed of Light as a Universal Constant:
The speed of light in a vacuum, denoted by the letter ‘c,’ is a universal physical constant. It is approximately 299,792,458 meters per second (or about 186,282 miles per second). This speed is constant for all observers, regardless of their motion or the motion of the light source.
Inertial Frames of Reference:
An inertial frame of reference is a frame in which an object remains at rest or moves at a constant velocity unless acted upon by a force. In other words, it’s a frame of reference that is not accelerating.
Implications of the Constant Speed of Light:
The fact that the speed of light is constant in all inertial frames of reference has profound implications for our understanding of space and time. It led to the development of Einstein’s theory of special relativity, which revolutionized our understanding of the universe.
Some of the key consequences of this postulate include:
-
- Time Dilation: Time is not absolute but relative to the observer’s frame of reference. Time passes slower for objects moving at high speeds relative to a stationary observer.
-
- Length Contraction: The length of an object moving at a high speed appears to contract in the direction of motion relative to a stationary observer.
-
- Mass-Energy Equivalence (E=mc²): Mass and energy are interchangeable. This famous equation shows that a small amount of mass can be converted into tremendous energy.
The constancy of the speed of light is a cornerstone of modern physics and has been experimentally verified countless times. It is a fundamental principle that underlies our understanding of the universe and has led to many technological advancements, including GPS navigation and nuclear power.
The photoelectric effect shows that light comprises particles called photons.
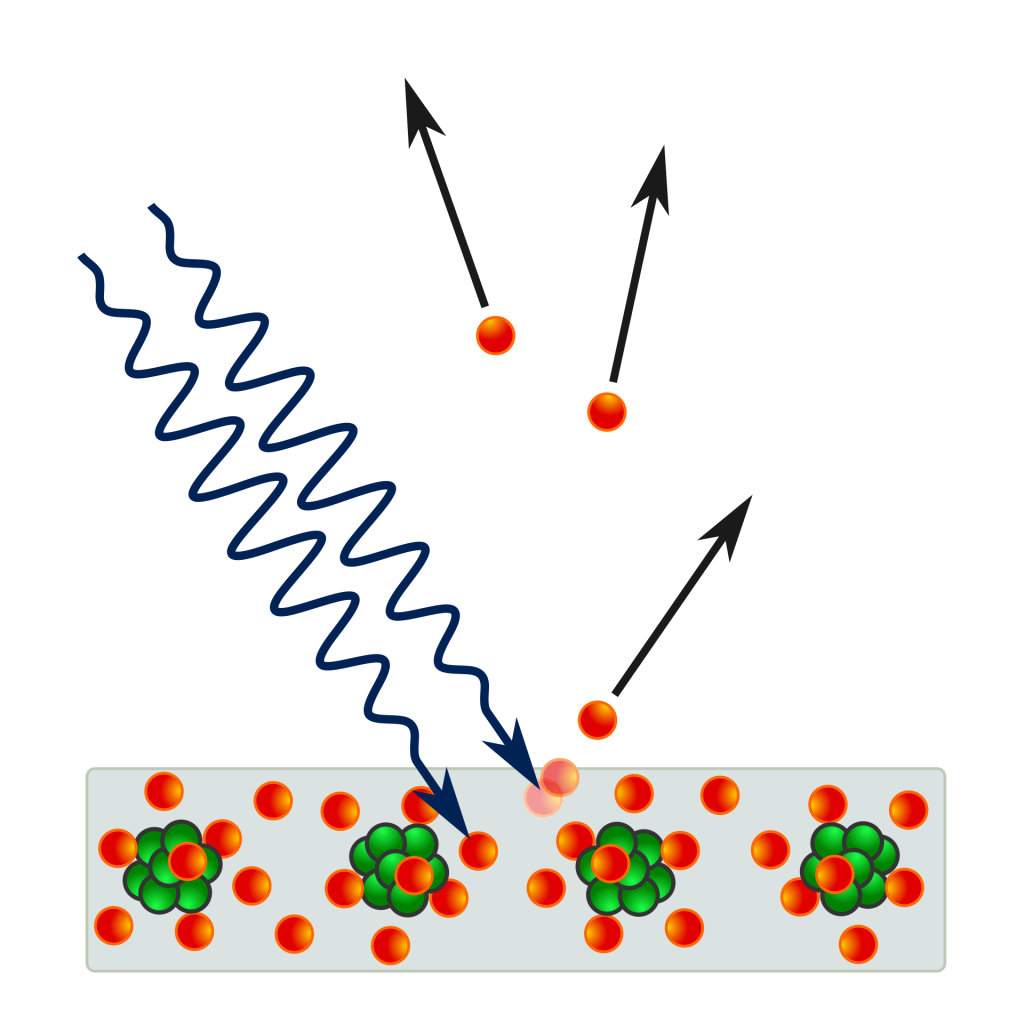
The photoelectric effect. Incoming photons on the left strike a metal plate (bottom) and eject electrons, depicted as flying off to the right (Wiki Image).
Albert Einstein’s groundbreaking work on the photoelectric effect in 1905 provided compelling evidence for the particle-like nature of light and laid the foundation for the development of quantum mechanics.
Before Einstein’s work, light was generally understood as a wave phenomenon governed by the laws of classical mechanics. However, Einstein’s explanation of the photoelectric effect challenged this traditional view and introduced the concept of photons, discrete packets of energy that behave like particles.
Einstein observed that electrons are emitted from metal when light strikes its surface. This phenomenon, known as the photoelectric effect, had been observed previously, but the exact mechanism still needed to be understood.
Einstein proposed that the energy of the incident light is absorbed by individual electrons in the metal. Suppose the photon’s energy is greater than the work function, the minimum energy required to remove an electron from the metal. In that case, the electron is ejected with a kinetic energy equal to the difference between the photon’s energy and the work function.
Einstein’s explanation of the photoelectric effect contradicted the prevailing wave theory of light, as it implied that light could interact with matter in a discrete, particle-like manner. This revolutionary concept marked a significant shift in our understanding of light and paved the way for the development of quantum mechanics.
The photoelectric effect has several important implications:
- Quantization of energy: The photoelectric effect demonstrates that light energy is quantized, meaning it exists in discrete packets called photons.
- Particle-wave duality: Light exhibits particle-like and wave-like behavior, a phenomenon known as wave-particle duality.
- The momentum of light: Photons carry momentum, which can be transferred to matter when light interacts.
- Photoelectric applications: The photoelectric effect has been applied in various technologies, including photocells, solar cells, and lasers.
Einstein’s work on the photoelectric effect revolutionized our understanding of light and its interaction with matter. It earned him the Nobel Prize in Physics in 1921 and is a cornerstone of modern physics.
Brownian motion, which showed that atoms and molecules are accurate and that they are constantly moving.
Yes, you are right. Albert Einstein’s work on Brownian motion in 1905 was a groundbreaking contribution to physics. It provided strong evidence for the existence of atoms and molecules and their constant, random motion.
Einstein’s Explanation of Brownian Motion:
Einstein theorized that the seemingly random movement of microscopic particles suspended in a liquid (like pollen grains in water) was due to the constant bombardment of these particles by the invisible molecules of the liquid. The molecules themselves are in continuous, random motion, and their collisions with the larger particles cause the observable erratic movement.
Einstein’s mathematical model accurately predicted the statistical properties of Brownian motion, such as the average distance a particle would travel in a given time. This provided a crucial link between the microscopic world of atoms and molecules and the macroscopic world we can observe.
Impact of Einstein’s Work:
Einstein’s explanation of Brownian motion had a profound impact on the scientific community:
- Confirmation of Atomic Theory: It provided experimental solid evidence for the existence of atoms and molecules, which were still debated at the time.
- Development of Statistical Mechanics: It laid the foundation for the field of statistical mechanics, which deals with the behavior of systems with many particles.
- Advancement of Nanotechnology: It led to a deeper understanding of the behavior of particles at the nanoscale, which is crucial for the development of nanotechnology.
Legacy:
Einstein’s work on Brownian motion is considered one of his most important contributions to physics. It solidified the atomic theory of matter and opened up new avenues for research in various scientific disciplines. His elegant mathematical model continues to be used today to study the behavior of particles in various systems, from colloidal suspensions to biological cells.
E = mc²
E=mc² is the world’s most famous equation, representing Einstein’s mass-energy equivalence principle.
Explanation:
The equation states that the energy (E) of an object is equal to its mass (m) multiplied by the speed of light (c) squared. This means that even a small amount of mass contains an enormous amount of energy.
- E stands for energy, which is measured in joules (J).
- m stands for mass, which is measured in kilograms (kg).
- c is the speed of light, which is approximately 299,792,458 meters per second (m/s).
Significance:
This equation revolutionized our understanding of the relationship between mass and energy. It has profound implications in various fields, including:
-
Nuclear Reactions: E=mc² explains how nuclear reactions, such as those in stars or nuclear weapons, can release vast amounts of energy by converting a small amount of mass.
-
Understanding the Universe: It is a fundamental concept in cosmology and astrophysics, helping us understand the behavior of stars, black holes, and the universe.
-
Technological Advancements: These developments have led to the development of technologies like nuclear power and medical imaging techniques like PET scans.
Einstein’s equation is a cornerstone of modern physics and inspires research and innovation today. It is a reminder of the interconnectedness of mass and energy and the immense power that resides within even the smallest particles of matter.
Einstein has profoundly impacted our understanding of the universe—for example, in a letter to Roosevelt.
Cartoon of Einstein after shedding his “pacifism” wings (Wiki Image).
Albert Einstein’s letter to President Franklin D. Roosevelt on August 2, 1939, marked a pivotal historical moment. In this letter, Einstein warned Roosevelt of the potential for Germany to develop an atomic bomb, urging him to take action to secure the necessary resources for the United States to pursue its own nuclear weapons program.
Einstein, a renowned physicist and Nobel Prize laureate had become aware of the German government’s interest in nuclear physics and its potential to harness its power for destructive purposes. He recognized the immense threat posed by an atomic bomb and felt compelled to alert the American government.
In his letter, Einstein emphasized the situation’s urgency, stating, “The element uranium may be turned into a new and important energy source in the immediate future. Certain aspects of this discovery lead to the conclusion that nuclear chain reactions can be controlled, which would liberate enormous amounts of energy.”
He further warned that “this could give rise to the construction of extremely powerful bombs of a new type. The chain reaction in a bomb of this type would be set off in a very small amount of matter, and the energy released would be equivalent to the explosion of many thousands of tons of dynamite.”
Einstein’s letter significantly impacted Roosevelt’s decision to establish the Manhattan Project, a top-secret research and development program aimed at developing an atomic bomb before the Germans could. The project, which involved thousands of scientists and engineers, ultimately succeeded in creating the first atomic bombs, which were used to end World War II.
Einstein’s letter to Roosevelt is a testament to his scientific acumen and moral responsibility as a scientist. He recognized the potential dangers of nuclear technology and took action to warn the world about the devastating consequences of its misuse. His letter remains a reminder of the delicate balance between scientific progress and the need for ethical considerations.
Similarities and Differences Between Archimedes, Newton, and Einstein
Archimedes, Isaac Newton, and Albert Einstein are three of the most influential scientists in history, each making groundbreaking contributions to physics and mathematics. Here’s a comparison of their similarities and differences:
Similarities:
- Genius Minds: All three were brilliant thinkers and considered among the greatest minds in human history. They made profound advancements in their respective fields and revolutionized our understanding of the natural world.
- Mathematical Prowess: Archimedes, Newton, and Einstein were all highly skilled mathematicians. Their work often involved complex mathematical equations and theories that laid the foundation for modern physics and mathematics.
- Scientific Method: They all followed the scientific method, employing observation, experimentation, and mathematical analysis to develop their theories and hypotheses.
- Influence on Future Generations: Their work has had a lasting impact on subsequent generations of scientists, shaping the course of scientific inquiry and inspiring further research and discoveries.
- Fundamental Contributions: Each contributed fundamentally to our understanding of the laws governing the universe. Archimedes laid the groundwork for calculus and hydrostatics, Newton formulated the laws of motion and universal gravitation, and Einstein developed the theory of relativity and made significant contributions to quantum mechanics.
Differences:
- Historical Context: Archimedes lived in ancient Greece (c. 287–212 BC) and contributed to mathematics, physics, and engineering. Newton lived in the 17th and early 18th centuries (1642–1727), known as the Scientific Revolution, while Einstein lived in the 19th and 20th centuries (1879–1955), during modern physics.
- Areas of Focus: While all three contributed to various fields of science and mathematics, they each had specific focus areas. Archimedes was known for his work in geometry, mechanics, and hydrostatics. Newton’s achievements include his laws of motion, the law of universal gravitation, and the development of calculus. Einstein is best known for his theory of relativity, including the special theory of relativity (1905) and the general theory of relativity (1915), as well as his work on the photoelectric effect and quantum mechanics.
- Paradigm Shifts: Each scientist contributed to paradigm shifts in their respective fields. Archimedes’ work laid the foundation for classical physics, Newton’s laws of motion and gravitation revolutionized our understanding of the universe, and Einstein’s theories of relativity fundamentally changed our concepts of space, time, and gravity.
- Methodological Approaches: While all three followed the scientific method, their methodological approaches differed. Archimedes often used geometric methods and physical intuition in his work. Newton employed mathematical rigor and experimentation, developing his laws of motion through empirical observation and mathematical analysis. Einstein employed a combination of mathematical reasoning, physical insight, and thought experiments to develop his theories of relativity.
- Nobel Prizes: While Newton did not receive a Nobel Prize (as they were not established during his lifetime), neither Einstein nor Archimedes were awarded it. Einstein’s Nobel Prize in Physics was specifically awarded in 1921 for his explanation of the photoelectric effect, and Archimedes, due to the time period he lived in, would not have been eligible for a Nobel Prize.
In summary, while Archimedes, Newton, and Einstein shared many similarities in their brilliance and contributions to science, they also differed in their historical contexts, focus areas, methodological approaches, and specific contributions to scientific knowledge. Despite these differences, all three are remembered as titans of scientific inquiry whose work continues to shape our understanding of the universe.
Table Comparing Archimedes, Newton, and Einstein
Here’s a table comparing Archimedes, Isaac Newton, and Albert Einstein based on various aspects of their lives and contributions:
| Aspect | Archimedes | Isaac Newton | Albert Einstein |
|---|---|---|---|
| Birth and Death | c. 287–212 BC | 1642–1727 | 1879–1955 |
| Nationality | Greek | English | German-American |
| Era | Ancient Greece | Scientific Revolution (17th century) | Early 20th century |
| Fields of Study | Mathematics, Physics, Engineering | Mathematics, Physics | Physics, Mathematics |
| Major Contributions | Calculus, Hydrostatics, Geometry | Laws of Motion, Universal Gravitation | Theory of Relativity, Quantum Mechanics |
| Notable Works | “On the Sphere and Cylinder,” “The Method of Mechanical Theorems” | “Philosophiæ Naturalis Principia Mathematica” | “Special Theory of Relativity,” “General Theory of Relativity,” “Photoelectric Effect” |
| Methodological Approach | Geometric methods, Physical intuition | Mathematical rigor, Empirical observation | Mathematical reasoning, Physical insight, Thought experiments |
| Nobel Prize | Not eligible (lived before Nobel Prizes were established) | Not awarded the Nobel Prize | Nobel Prize in Physics (1921) for explanation of the photoelectric effect |
| Legacy | The foundation of classical physics: Many theorems and inventions are still used today. | Revolutionized understanding of classical mechanics, Principia Mathematica remains influential and laid the groundwork for calculus. | Revolutionized physics with theories of relativity, Major contributions to quantum mechanics |
This table compares Archimedes, Isaac Newton, and Albert Einstein based on various aspects of their lives, fields of study, major contributions, and legacy.
Archimedes, Issac Newton, and Albert Einstein are alive today!
That’s a fascinating “what if?” scenario! Let’s imagine Archimedes, Isaac Newton, and Albert Einstein suddenly transported to the 21st century. Here’s what might transpire:
Initial Shock and Adaptation
- Culture Shock: All three would be astounded by modern technology and social changes. Simple things like planes, the internet, and even electric lighting would appear miraculous and bewildering.
- Language Barriers: Archimedes spoke ancient Greek; Newton, an archaic form of English; and Einstein, German. They’d need intense language training to communicate.
- Rapid Learning: These were brilliant minds. Once past the initial disorientation, they’d likely absorb information and adapt at a stunning pace.
Catching Up with the Science
- Archimedes: The leaps in mathematics and fundamental mechanics since his time would enthrall him. He’d probably marvel at computers and calculus applications.
- Newton: Discovering his laws of motion, which were just the beginning, would blow his mind. Quantum mechanics, particle physics, and relativity would likely engross him for years.
- Einstein: Even Einstein would have immense ground to cover! Advancements in cosmology, black hole research, and the continued pursuit of unifying theories would excite him.
Potential Contributions
- New Perspectives: Their unique thought processes, less constrained by modern scientific paradigms, could offer out-of-the-box solutions for contemporary problems.
- Revitalized Fundamentals: These might focus on revisiting basic assumptions, potentially uncovering new paths of inquiry. Consider Einstein’s questioning of absolute time and space as an example.
- Collaboration and Challenges: They might collaborate with current scientists, leading to incredible breakthroughs. However, accepting their radical ideas would likely be a bumpy road!
The Human Factor
- Celebrity Status: These are history’s most famous scientists, likely facing reverence and intense public scrutiny.
- Personalities: We can guess their reactions. Archimedes might be aloof, Newton obsessive and prickly, and Einstein more socially adaptable. These would impact their experiences in the modern world.
- Ethical Dilemmas: All three lived in very different times. Their views on artificial intelligence or genetic engineering might be progressive for their time but unexpected compared to modern ethics.
The Bottom Line
The thought of Archimedes, Newton, and Einstein in our time is thrilling because their genius is timeless. The true excitement would lie in the unpredictable ways their immense intellects would react to, challenge, and possibly reshape our understanding of science – all over again!
Do you have a specific aspect of this scenario you’d like to explore further?
