AI: Galileo Galilei, Johannes Kepler, and Christiaan Huygens Compared: The Telescope Revolutionized Astronomy in the 17th Century

 

Galileo Galilei, Johannes Kepler, and Christiaan Huygens: The telescope revolutionized astronomy in the 17th century

You are correct. The invention and application of the telescope in the 17th century utterly revolutionized astronomy, and Galileo Galilei, Johannes Kepler, and Christiaan Huygens were central figures in this transformation, each contributing in distinct yet complementary ways:

1. Galileo Galilei (1564–1642): While not the inventor of the telescope, Galileo was a crucial early adopter who significantly improved its design and, most importantly, systematically turned it towards the heavens from 1609 onwards. His observations provided a flood of new evidence that shattered ancient Aristotelian and Ptolemaic cosmological views:  
   • He discovered the craters and mountains on the Moon, proving it wasn’t a perfect celestial sphere.  
   • He observed Jupiter’s four largest moons (the Galilean moons), demonstrating that celestial bodies could orbit something other than Earth.  
   • He documented the phases of Venus, which strongly supported the Copernican heliocentric model.
   • He resolved the Milky Way into countless individual stars and observed sunspots, challenging the idea of a perfect, unchanging heavens. His widely publicized discoveries in works like Sidereus Nuncius (Starry Messenger, 1610) were pivotal in shifting astronomical thought.  
2. Johannes Kepler (1571–1630): Primarily known for his laws of planetary motion (derived from Tycho Brahe’s pre-telescopic data), Kepler was also an early and enthusiastic adopter of the telescope and a key theorist of optics:  
   • He quickly confirmed Galileo’s discoveries, lending them crucial support from an established astronomer.
   • He made significant contributions to optical theory in his Astronomiae Pars Optica (1604) and Dioptrice (1611), explaining how lenses form images.  
   • He designed an improved version of the refracting telescope (the “Keplerian telescope”) using two convex lenses, which offered a wider field of view and higher magnification potential, becoming the basis for most later astronomical refractors. His work provided the precise mathematical framework for the new heliocentric universe that telescopic observations were revealing.  
3. Christiaan Huygens (1629–1695): Representing the next wave of telescopic astronomers, Huygens made significant advancements both in telescope construction and observational discoveries:  
   • He and his brother became master lens grinders, producing telescopes of superior quality and power.
   • This allowed him to discover Saturn’s largest moon, Titan (1655).
   • Crucially, he was the first to correctly interpret Saturn’s strange appearance as being surrounded by a thin, flat ring system that did not touch the planet (published in Systema Saturnium, 1659), solving a puzzle that had baffled Galileo and others.
   • He developed the Huygenian eyepiece, improving telescope performance.  
   • Beyond direct astronomical observation, his invention of the pendulum clock (1656) provided the first reliable way to keep accurate time, essential for precise astronomical measurements. His work on the wave theory of light (Traité de la Lumière, 1690) also had profound implications for understanding the universe.

Galileo’s groundbreaking observations, Kepler’s mathematical laws and optical theories, and Huygens’ instrumental advancements and further discoveries cemented the telescope’s role as an indispensable tool, fundamentally changing astronomy methods, scope, and understanding in the 17th century and beyond.

Galileo Galilei (1564–1642)

Galileo Galilei

(Wiki Image By Justus Sustermans – http://collections.rmg.co.uk/collections/objects/14174, Public Domain, https://commons.wikimedia.org/w/index.php?curid=62614082) 

Galileo Galilei Quotes

Galileo Galilei was a pivotal figure in the Scientific Revolution, and many insightful and often defiant statements are attributed to him. Here is a selection of his well-known quotes:

1. “Philosophy [i.e., science] is written in this grand book, the universe, which stands continually open to our gaze. But the book cannot be understood unless one first learns to comprehend the language and read the letters in which it is composed. It is written in the language of mathematics, and its characters are triangles, circles, and other geometric figures without which it is humanly impossible to understand a single word of it; without these, one wanders about in a dark labyrinth.” (From The Assayer, 1623)  
2. “And yet it moves.” (Eppur si muove) (Famously attributed to Galileo after being forced to recant his heliocentric views by the Inquisition in 1633, implying the Earth still orbits the Sun. However, this is likely apocryphal and first appeared in print over a century after his death.)
3. “I do not feel obliged to believe that the same God who has endowed us with sense, reason, and intellect has intended us to forgo their use.” (Often cited, a sentiment expressed in his Letter to the Grand Duchess Christina, 1615)  
4. “The Bible shows the way to go to heaven, not the way the heavens go.” (This is attributable to Galileo summarizing a sentiment he expressed, possibly quoting Cardinal Baronio, in defense of separating scientific inquiry from literal scriptural interpretation.)
5. “In questions of science, the authority of a thousand is not worth the humble reasoning of a single individual.”
6. “All truths are easy to understand once they are discovered; the point is to discover them.”
7. “Measure what is measurable, and make measurable what is not so.” (A guiding principle often attributed to him, reflecting his emphasis on quantification.)
8. “The Milky Way is nothing else but a mass of innumerable stars planted together in clusters.” (From Sidereus Nuncius (Starry Messenger), 1610, describing his telescopic observations.)
9. “It is surely harmful to souls to make it a heresy to believe what is proved.” (Reflecting his frustration with the Church’s stance on Copernicanism.)
10. “I have never met a man so ignorant that I couldn’t learn something from him.”
11. “Where the senses fail us, reason must step in.”
12. “Facts which at first seem improbable will, even on scant explanation, drop the cloak which has hidden them and stand forth in naked and simple beauty.”  

These quotes capture Galileo’s commitment to observation, mathematical reasoning, intellectual freedom, and his profound impact on our understanding of the universe.

 

Galileo Galilei YouTube Video

Galileo – Physicist | Mini Bio | BIO

Galileo Galilei: Father of Modern Science

Galileo Galilei – in a nutshell

 

Galileo Galilei History

Cristiano Banti‘s 1857 painting Galileo facing the Roman Inquisition

(Wiki Image By Cristiano Banti – http://www.law.umkc.edu/faculty/projects/ftrials/galileo/galileotrial.jpghttps://www.newscientist.com/article/mg22530043-300-popes-impending-call-for-climate-action-is-refreshing/ image, Public Domain, https://commons.wikimedia.org/w/index.php?curid=631170) 

 

Galileo Galilei (February 15, 1564 – January 8, 1642) was an Italian astronomer, physicist, engineer, philosopher, and mathematician who played a pivotal role in the Scientific Revolution of the 17th century. He is often referred to as the “father of observational astronomy,” the “father of modern physics,” the “father of the scientific method,” and even the “father of modern science.”  

Here’s an overview of his history:

1. Early Life and Education (1564-1589):
   • Born in Pisa, Italy, Galileo was the son of Vincenzo Galilei, a lutenist, composer, and music theorist.  
   • He initially studied medicine at the University of Pisa at his father’s urging, but soon found his true passion in mathematics and “natural philosophy” (physics).
   • During this period, he made early observations about the pendulum’s isochronism (the idea that the period of swing is independent of the amplitude, though this is only approximately true for small swings). He left the university in 1585 without a degree due to financial reasons.  
2. Early Academic Career and Scientific Work (1589-1609):
   • He secured a teaching position in mathematics at the University of Pisa in 1589 and later at the more prestigious University of Padua in 1592, where he remained for 18 years.  
   • In Padua, he taught geometry, mechanics, and astronomy. He conducted experiments on falling bodies, reputedly (though perhaps apocryphally) by dropping objects from the Leaning Tower of Pisa, and through experiments with inclined planes. These led him to formulate early ideas about acceleration and the laws of motion.  
   • He invented or improved various practical instruments, including a military compass and an early thermoscope (a precursor to the thermometer).  
3. Telescopic Discoveries and Rise to Fame (1609-1616):
   • In 1609, Galileo heard about the invention of the telescope (or “spyglass”) in the Netherlands by figures like Hans Lippershey. He quickly understood its principles and constructed his own, significantly improving its magnification (eventually up to about 30x).  
   • He was among the first to turn the telescope to the heavens, and his observations were revolutionary:
     • The Moon: He observed that its surface was not smooth and perfect as Aristotelian cosmology held, but rugged, with mountains and craters.  
     • The Milky Way: He resolved it into a multitude of individual stars.
     • Jupiter’s Moons: In January 1610, he discovered four celestial bodies orbiting Jupiter, which he named the “Medicean Stars” (now known as the Galilean moons: Io, Europa, Ganymede, and Callisto). This was crucial evidence against the idea that all celestial bodies must orbit the Earth.  
     • Phases of Venus: He observed Venus going through a full set of phases, similar to Earth’s Moon. This could only be explained if Venus orbited the Sun, not the Earth, providing strong support for the Copernican heliocentric model.  
     • Sunspots: He observed and made detailed drawings of sunspots, inferring the Sun’s rotation.  
   • He published these findings in his groundbreaking book Sidereus Nuncius (Starry Messenger) in 1610, which brought him international fame and a position as mathematician and philosopher to the Grand Duke of Tuscany in Florence.  
4. Advocacy of Copernicanism and First Conflict with the Church (1610-1616):  
   • Galileo’s discoveries provided strong observational evidence for Nicolaus Copernicus’s heliocentric theory (Sun-centered universe), which contradicted the long-established geocentric (Earth-centered) model of Ptolemy and Aristotle, then supported by the Catholic Church.  
   • His increasingly vocal support for Copernicanism drew opposition from some academics and churchmen.  
   • In 1616, the Church’s Holy Office formally declared heliocentrism “foolish and absurd in philosophy, and formally heretical since it explicitly contradicts in many places the sense of Holy Scripture.” Galileo was warned by Cardinal Bellarmine not to “hold or defend” the Copernican doctrine, though he was permitted to discuss it hypothetically.  
5. Dialogue Concerning the Two Chief World Systems and Trial (1616-1633):  
   • After a period of relative quiet, Galileo, with the permission of the new Pope Urban VIII (formerly Cardinal Maffeo Barberini, an admirer of Galileo), published his Dialogue Concerning the Two Chief World Systems in 1632.  
   • While ostensibly a neutral discussion between advocates of the Ptolemaic and Copernican systems, the book was widely seen (and intended) as a powerful defense of heliocentrism. The character Simplicio, who defended the geocentric view, was perceived by some, including the Pope, as a caricature of themselves or Aristotelian philosophers.
   • This led to Galileo’s summons before the Roman Inquisition in 1633. He was found “vehemently suspect of heresy” for having held and defended the Copernican doctrine after the 1616 admonition.  
   • He was forced to abjure (recant) his heliocentric views and was sentenced to house arrest for the remainder of his life. His Dialogue was banned.
6. Later Years and Two New Sciences (1633-1642):
   • Despite being under house arrest in his villa in Arcetri, near Florence, and eventually going blind, Galileo continued his scientific work.  
   • His final major work, Discourses and Mathematical Demonstrations Relating to Two New Sciences (often called Two New Sciences), was published in Leiden (Holland) in 1638. This book summarizes his decades of work on kinematics (the science of motion) and the strength of materials, laying the groundwork for modern physics and engineering. Many historians consider it his most important scientific contribution.  
7. Death and Legacy:
   • Galileo died in Arcetri on January 8, 1642.  
   • His contributions to observational astronomy, physics, the development of the scientific method (emphasizing experiment and mathematical analysis), and his courageous stand for intellectual inquiry (despite its consequences) have secured his place as a pivotal figure in the history of science and the Scientific Revolution. The Catholic Church eventually acknowledged the errors in his trial, notably in a speech by Pope John Paul II in 1992.

 

Galileo Galilei’s Discoveries Table

Okay, here is a table summarizing some of Galileo Galilei’s major scientific discoveries and contributions:

Discovery/Contribution	Significance/Details
Astronomical (Telescopic) Discoveries
Mountains and Craters on the Moon	Observed (c. 1609) that the Moon’s surface was not perfectly smooth as per Aristotelian cosmology, but rugged and Earth-like. This challenged the idea of perfect celestial bodies.
Four Largest Moons of Jupiter (Galilean Moons)	Discovered Io, Europa, Ganymede, and Callisto (1610). This showed that celestial bodies could orbit a planet other than Earth, challenging the geocentric model.
Phases of Venus	Observed Venus going through a full set of phases, similar to Earth’s Moon. This was strong evidence that Venus orbits the Sun, supporting the Copernican heliocentric model.
Sunspots	Observed dark spots on the Sun’s surface and tracked their movement, inferring the Sun’s rotation and challenging the notion of the Sun’s perfection.
Composition of the Milky Way	Resolved the Milky Way from a nebulous band into a vast collection of countless individual stars, expanding the known scale of the universe.
Saturn’s “Appendages”	Observed Saturn as having strange “handles” or “ears.” His telescope wasn’t powerful enough to resolve them clearly as rings (later identified by Huygens).
Physics and Mechanics
Law of Falling Bodies	Formulated the principle that, neglecting air resistance, all objects fall with the same constant acceleration, regardless of their mass. Challenged Aristotelian physics.
Principle of Inertia	Developed an early understanding of inertia: a body in motion will stay in motion unless acted upon by a force. A precursor to Newton’s First Law.
Projectile Motion	Determined that the path of a projectile is a parabola, resulting from the combination of uniform horizontal motion and uniformly accelerated vertical motion.
Isochronism of the Pendulum	Discovered that the period of a pendulum’s swing is nearly independent of its amplitude (for small swings), leading to its use in timekeeping.
Inventions/Improvements
Improved Refracting Telescope	While not the inventor, Galileo significantly improved telescope designs (up to ~30x magnification), making his groundbreaking astronomical observations possible.
Thermoscope	Invented an early type of thermometer that could indicate temperature changes (though not a standardized scale).
Military and Geometric Compass	Developed and sold a practical calculating instrument for various military and surveying applications.

Export to Sheets

These discoveries and contributions were fundamental to the Scientific Revolution, shifting understanding from ancient Greek philosophy towards observation, experimentation, and mathematical analysis.

 

Telescopic Discoveries

Galileo Galilei: Mountains and craters of the moon

Here’s an image related to Galileo Galilei’s observations of the moon’s mountains and craters:

Galileo Galilei’s telescopic observations of the Moon, particularly his identification of its mountains and craters, were among his earliest and most revolutionary discoveries, fundamentally challenging the long-held views of the cosmos.  

Here’s a summary of this crucial work:

1. Timing and Method of Observation:
   • Galileo began his systematic telescopic observations of the Moon in late 1609 and early 1610.
   • He used telescopes he had significantly improved, which offered magnifications of up to around 20-30 times.
   • Crucially, Galileo applied his understanding of chiaroscuro (the use of light and shadow in art, with which he was familiar due to his artistic training) to interpret the patterns of light and darkness he saw on the lunar surface.  
2. Key Findings – An Imperfect, Earth-like Moon:
   • Mountains and Valleys: Contrary to the prevailing Aristotelian belief that celestial bodies were perfect, smooth spheres made of a special, unblemished fifth element (aether), Galileo observed that the Moon’s surface was rugged, uneven, and varied, much like the Earth’s. He saw bright spots in the dark portion of the Moon near the terminator (the dividing line between the illuminated and dark parts), which he correctly interpreted as mountain peaks catching the sunlight while the surrounding lower regions were still in shadow. Similarly, he observed dark spots in the illuminated part, which he identified as valleys or craters.  
   • Craters: He observed numerous circular depressions, which we now know as craters.  
   • Estimation of Mountain Heights: By observing the length of the shadows cast by lunar mountains near the terminator and applying simple geometry, Galileo was able to estimate their heights. He concluded that some lunar mountains were comparable in height to, or even taller than, mountains on Earth (he estimated some to be over four miles high).
   • Earthshine: He also correctly explained “earthshine” (the faint glow on the dark portion of the Moon) as sunlight reflected from the Earth onto the Moon.
3. Contradiction to Prevailing Cosmological Views:
   • These observations were a direct assault on the Aristotelian concept of a perfect, unchanging celestial realm distinct from the corruptible, changeable terrestrial realm.
   • By showing the Moon to be a world with a physical topography similar to Earth’s, Galileo blurred this fundamental distinction and suggested that celestial bodies might be made of similar “earthly” matter.
4. Publication in Sidereus Nuncius (Starry Messenger):  
   • Galileo published these groundbreaking lunar observations, complete with detailed drawings and engravings of what he saw, in his short but immensely impactful treatise, Sidereus Nuncius, in March 1610. This book, which also announced his discovery of Jupiter’s moons and the stellar composition of the Milky Way, caused a sensation across Europe.  
5. Significance:
   • Shattered Ancient Beliefs: The discovery of an imperfect, Earth-like Moon was a major blow to the foundations of Aristotelian cosmology.
   • Paved the Way for New Cosmologies: It lent support to the idea that Earth might itself be a planet, similar in nature to other celestial bodies, which was a key tenet of the Copernican heliocentric model.
   • Demonstrated Telescope’s Power: It showcased the revolutionary capability of the telescope to reveal new realities about the universe, challenging traditional authority and emphasizing empirical observation.
   • Fueled the Scientific Revolution: This discovery was a crucial early step in the broader Scientific Revolution, encouraging further observation and re-evaluation of ancient doctrines.

It’s worth noting that the English astronomer Thomas Harriot also made telescopic drawings of the Moon around the same time (even slightly earlier in July 1609), but Galileo’s observations were more detailed, his interpretations more profound in their cosmological implications, and, critically, his findings were rapidly published and widely disseminated, leading to a much greater immediate impact.

 

Galileo Galilei: The four largest moons are Jupiter’s

Here’s an image related to Galileo Galilei’s discovery of Jupiter’s four largest moons:

Galileo Galilei’s most famous and impactful discovery was that Jupiter had four large moons orbiting it. This was a groundbreaking observation made with his improved telescope.  

Here are the key details about this discovery:

1. Date of Discovery: Galileo first observed what he initially thought were three small, fixed stars near Jupiter on January 7, 1610. Over subsequent nights, he continued to observe them and noticed their positions changed relative to Jupiter in a way inconsistent with them being fixed stars. By January 13, 1610, he had observed a fourth such “star” and had concluded that these four bodies were moons orbiting Jupiter.  
2. Method of Discovery:
   • Galileo used a significantly improved refracting telescope capable of magnifying objects about 20 to 30 times.
   • He meticulously tracked the positions of these four “star-like” objects night after night, sketching their locations relative to Jupiter. He noted that they appeared and disappeared as they moved around and behind the planet.  
3. Galileo’s Interpretation: He quickly and correctly deduced that these were not stars but celestial bodies revolving around Jupiter, much like Earth’s Moon revolves around Earth. This was a radical idea at the time.  
4. Naming:
   • Galileo initially wanted to name them “Cosmica Sidera” (Cosimo’s Stars), but after seeking patronage from the powerful Medici family, he named them “Medicea Sidera” (Medicean Stars) in honor of Cosimo II de Medici, the Grand Duke of Tuscany, and his three brothers.  
   • The individual mythological names used today—Io, Europa, Ganymede, and Callisto—were proposed later by Simon Marius (who also claimed independent discovery of the moons around the same time) at Johannes Kepler’s suggestion. These names eventually became standard.  
5. Publication:
   • Galileo announced his discovery of Jupiter’s moons, observations of the Moon’s surface, and observations of the Milky Way’s composition in his groundbreaking treatise Sidereus Nuncius (Starry Messenger), published in Venice in March 1610.  
6. Significance of the Discovery:
   • Challenged Geocentric Model: This discovery was monumental because it provided clear evidence that not everything in the heavens orbited the Earth. The prevailing Ptolemaic (Earth-centered) model held that Earth was the center of all celestial motion.  
   • Supported Copernican Model (Heliocentrism): The existence of moons orbiting another planet offered a miniature model of the Copernican solar system, where planets (like Jupiter with its moons) orbited the Sun. It made the idea of Earth being just another planet with its own moon, orbiting a central body, more plausible.  
   • Demonstrated the Power of the Telescope: It showcased the revolutionary potential of the telescope to reveal new and unexpected phenomena in the universe, beyond what could be seen with the naked eye.
   • Expanded the Known Solar System: It added four new celestial bodies to the known components of the solar system.  

Galileo’s discovery of Jupiter’s four largest moons was a critical piece of observational evidence that significantly contributed to the shift from a geocentric to a heliocentric understanding of the cosmos during the Scientific Revolution.

 

Galileo Galilei: Phases on Venus

Here’s an image related to Galileo Galilei’s discovery of the phases of Venus:

 

Galileo Galilei’s telescopic observation of the full set of phases of Venus in late 1610 was a pivotal discovery that provided strong evidence against the prevailing geocentric (Earth-centered) Ptolemaic system and supported models where Venus orbits the Sun.  

Here’s a breakdown of this significant discovery:

1. The Observation:
   • Galileo observed Venus over several months in late 1610 and early 1611 using his improved telescope.  
   • He saw that Venus exhibited a complete sequence of phases, similar to those of Earth’s Moon – it appeared as a crescent, then half-lit, then gibbous (more than half-lit), and approached a nearly full phase (though “full” Venus is hard to see as it’s on the far side of the Sun and close to it in the sky).  
   • Crucially, he observed Venus appearing small and nearly full when it was on the far side of the Sun from Earth, and larger and crescent-shaped when it was on the near side.
2. Contradiction with the Ptolemaic Model:
   • The strictly Earth-centered Ptolemaic system placed Venus’s (and Mercury’s) orbit on an epicycle whose center always lay on the line connecting the Earth and the Sun, with Venus always positioned between Earth and the Sun.  
   • In such a model, Venus, as viewed from Earth, should only ever display crescent and “new” phases. It could never appear gibbous or full because the fully illuminated side of Venus would always face away from Earth.
   • Galileo’s observation of a gibbous and near-full Venus contradicted this Ptolemaic model prediction.  
3. Support for a Sun-Centered Orbit for Venus:
   • The observed full set of phases was entirely consistent with a model where Venus orbits the Sun.
     • We see a crescent (or new phase) when Venus is between Earth and the Sun.
     • When Venus is on the far side of the Sun from Earth, we see it as nearly full (though smaller in apparent size due to greater distance).
   • The Copernican heliocentric model predicted this. It was also consistent with the Tychonic system (a hybrid model where planets orbit the Sun, which in turn orbits a stationary Earth).  
   • While not definitively proving the Earth itself moved, it decisively showed that the Ptolemaic arrangement for Venus was incorrect and that Venus must orbit the Sun.  
4. Announcement (Anagram):
   • To establish priority for his discovery while he continued to make more comprehensive observations, Galileo famously communicated his findings in December 1610 via an anagram to figures like Johannes Kepler.
   • The unscrambled Latin sentence was: “Cynthiae figuras aemulatur mater amorum” which translates to “The mother of loves [Venus] imitates the figures of Cynthia [the Moon].”  
5. Significance:
   • Strong Evidence Against Geocentrism: The observation of Venus’s full phases was one of the most direct and easily understood pieces of observational evidence that undermined the credibility of the Ptolemaic geocentric system.  
   • Support for Sun-Centered Models: It provided powerful support for cosmological models where Venus (and Mercury) orbited the Sun, such as the Copernican system.  
   • Impact on the Scientific Revolution: This discovery, along with Galileo’s other telescopic findings (moons of Jupiter, imperfections on the Moon and Sun), played a crucial role in the broader shift in scientific thought during the Scientific Revolution, moving towards a heliocentric understanding of the solar system based on empirical evidence.

Galileo’s observation of the phases of Venus was a landmark achievement, demonstrating the power of the telescope to test and falsify long-standing astronomical theories.

 

Galileo Galilei: Sunspots

Here’s an image related to Galileo Galilei’s discovery of sunspots:

 

Galileo Galilei’s telescopic observations of sunspots were another crucial contribution that challenged the prevailing Aristotelian cosmology of perfect and unchanging heavens.  

Here’s an overview of his work on sunspots:

1. Observation Period and Method:
   • Galileo began systematic observations of sunspots around 1610-1612, following his initial groundbreaking telescopic discoveries.
   • He initially observed the Sun directly through his telescope, likely using darkened glass filters, which was dangerous and could have contributed to his later blindness.
   • He soon adopted and popularized the safer method of projection: projecting the Sun’s image through the telescope onto a white screen or paper, where the sunspots could be viewed and sketched indirectly. This method also allowed for more detailed and consistent tracking.  
2. Galileo’s Key Observations and Interpretations:
   • Nature of Sunspots: He observed that these dark spots appeared on the surface of the Sun, changed their shapes, grew, shrank, and eventually disappeared. This mutable nature was contrary to the Aristotelian idea of the Sun being a perfect, unblemished celestial sphere.  
   • Location on or Near the Sun’s Surface: A critical argument Galileo made was that the sunspots were either on the Sun’s surface or very close to it, like clouds in its atmosphere. He reasoned this by observing their foreshortening as they approached the Sun’s limb (edge) and their consistent travel time across the disk. This interpretation directly contradicted others, like Christoph Scheiner, who initially proposed that sunspots might be small planets orbiting the Sun. Galileo argued that if they were distant planets, their apparent speed across the solar disk would not show such pronounced foreshortening effects.  
   • Solar Rotation: By carefully tracking the movement of sunspots across the Sun’s disk, their disappearance around one limb, and reappearance (if they lasted long enough) at the opposite limb, Galileo conclusively demonstrated that the Sun rotates on its axis. He estimated the rotation period to be approximately one lunar month (about 27-28 days).  
3. Publication:
   • Galileo published his detailed observations, drawings, and arguments concerning sunspots in his work Istoria e dimostrazioni intorno alle macchie solari e loro accidenti (History and Demonstrations Concerning Sunspots and their Properties), commonly known as the Letters on Sunspots, in 1613. This work was published by the Accademia dei Lincei in Rome.  
4. Priority and Disputes:
   • Galileo was not the only person to observe sunspots telescopically around this time. Other astronomers, including Thomas Harriot in England (from December 1610), Johannes Fabricius in Friesland (who published a pamphlet on sunspots in 1611), and the Jesuit astronomer Christoph Scheiner in Germany (from 1611), also made early observations.  
   • This led to priority disputes, most notably between Galileo and Scheiner. While Scheiner initially interpreted sunspots as satellites of the Sun (to preserve solar perfection), Galileo robustly argued for their nature as features on or near the solar surface. Scheiner later accepted Galileo’s view on their location, but the rivalry persisted.  
5. Significance of Galileo’s Sunspot Observations:
   • Challenged Aristotelian Cosmology: The existence of “blemishes” (spots) on the Sun and their changing nature directly contradicted the ancient Greek philosophical ideal of perfect, incorruptible, and unchanging celestial bodies.  
   • Evidence for Solar Rotation: Provided the first strong observational evidence that the Sun itself rotates.  
   • Furthered Heliocentric Argument (Indirectly): While not direct proof of heliocentrism, the discovery of another celestial body (the Sun) rotating, like the Earth was proposed to do in the Copernican model, made the idea of a rotating Earth seem less unique or implausible.
   • Demonstrated Scientific Method: Galileo’s careful observation, meticulous recording, and logical deduction from the behavior of sunspots exemplified his approach to scientific inquiry.

Galileo’s work on sunspots was another significant blow to the old cosmology and a key step in understanding the dynamic nature of the Sun.

 

Galileo Galilei: Composition of the Milky Way

Here’s an image related to Galileo Galilei’s discovery of the Milky Way’s composition:

 

Galileo Galilei, through his pioneering use of the telescope around 1609-1610, made a revolutionary discovery about the composition of the Milky Way.  

1. The Prevailing View Before Galileo:
   • To the naked eye, the Milky Way appears as a faint, hazy, or “milky” band of light stretching across the night sky.  
   • For centuries, its true nature was a subject of speculation. Ancient Greek philosophers like Anaxagoras and Democritus hypothesized that it might be composed of distant stars, but this was not a widely accepted or provable theory.  
   • Aristotle, whose views were highly influential, believed it to be an atmospheric phenomenon, a luminous vapor in the upper atmosphere.  
2. Galileo’s Telescopic Observation:
   • When Galileo turned his improved telescope towards the Milky Way, he resolved what had previously appeared as a nebulous cloud.  
   • His telescope revealed that the Milky Way was composed of a vast multitude of individual stars, so densely packed and faint that the naked eye could not distinguish them.  
   • He observed that wherever he pointed his telescope within the band of the Milky Way, he saw “nothing else but a mass of innumerable stars planted together in clusters.” He also found that many objects previously classified as “nebulous stars” or hazy patches were clusters of many faint stars.
3. Publication in Sidereus Nuncius (Starry Messenger):  
   • Galileo published this groundbreaking discovery, along with his observations of the Moon, Jupiter’s moons, and other celestial phenomena, in his short but hugely influential treatise Sidereus Nuncius in March 1610.  
4. Significance of the Discovery:
   • Resolved an Ancient Mystery: Galileo’s observation provided the first strong empirical evidence for the true nature of the Milky Way, settling a debate that had lasted for millennia.
   • Vastly Expanded the Universe: The realization that the Milky Way was made of countless stars dramatically increased the perceived scale of the universe and the sheer number of stars within it, far beyond what had been previously imagined.  
   • Demonstrated the Power of the Telescope: This discovery was a clear demonstration of the telescope’s revolutionary power to reveal aspects of the cosmos previously hidden from human senses.
   • Challenged Old Cosmology: Like his other telescopic findings, this contributed to the undermining of the Aristotelian and Ptolemaic cosmological models by revealing a universe far more complex and extensive than those models allowed.

Galileo’s resolution of the Milky Way into individual stars was a pivotal moment in the history of astronomy, fundamentally changing our perception of our galaxy and the universe beyond.

 

Galileo Galilei: Saturn’s “Appendages”

Here’s an image related to Galileo Galilei’s discovery of Saturn’s “appendages”:

When Galileo Galilei first turned his improved telescope towards Saturn in July 1610, he encountered a puzzling sight that he couldn’t fully resolve with the optical power available to him. Instead of a simple sphere like other planets, Saturn appeared to have strange “appendages” or “companions” on either side.  

Here’s a breakdown of Galileo’s observations and interpretations of Saturn’s “appendages”:

1. Initial Observations (1610):  
   • Galileo described Saturn as appearing “triple-bodied” (“altissimum planetam tergeminum observavi” – “I have observed the highest planet to be triple-formed”). He saw the central globe of Saturn flanked by two smaller, fainter celestial bodies, one on each side, almost touching it.  
   • He initially thought these might be two large moons or “servants” attending Saturn, similar to the moons he had discovered around Jupiter earlier that year. However, unlike Jupiter’s moons, these companions of Saturn did not appear to orbit the planet but remained fixed relative to it. He sometimes referred to them as “handles” or “ears.”  
2. The Mystery of Changing Appearances:
   • To Galileo’s profound confusion, when he observed Saturn again in 1612, these side “companions” or “appendages” had vanished. Saturn appeared as a solitary, round globe.  
   • This disappearance deeply perplexed him, leading him to question his own observations and even the nature of Saturn itself. He famously wrote, “Has Saturn, perhaps, devoured his own children?” alluding to the myth of the Roman god Saturn (Cronus in Greek mythology).
   • Later, around 1616, when he observed Saturn again, the appendages had reappeared, but they looked different, now more like two “half ellipses.”
3. Limitations of his Telescope:
   • Galileo’s telescopes, while revolutionary for their time (magnifying up to about 20-30 times), had limited resolution and optical quality compared to later instruments.  
   • They were not powerful enough to clearly distinguish the true nature of Saturn’s rings as a thin, flat system detached from the planet. What he saw as “appendages” were in fact the ansae (the visible extent) of the rings when they were more open to our line of sight. The “disappearance” occurred when Earth passed through the plane of Saturn’s rings, making them appear edge-on and too thin to be resolved by his telescope.  
4. Galileo’s Reaction and Record:
   • He documented his observations and his bafflement in letters and notes. He was genuinely puzzled by Saturn’s changing form, as it didn’t fit any known celestial behavior.  
   • To protect his claim to the initial puzzling observation while trying to understand it, he published an anagram in 1610, which, when unscrambled, described his “triple-formed” observation of Saturn.
5. Significance:
   • Although Galileo misinterpreted what he saw, he was the first human to telescopically observe Saturn’s unique and non-spherical appearance.  
   • His observations revealed that Saturn was different from other planets and posed a significant astronomical puzzle for nearly half a century.
   • It highlighted the limitations of early telescopes but also spurred further investigation into the nature of this distant planet.  

It was not until 1655-1659 that Christiaan Huygens, using a much more powerful telescope of his own making, correctly hypothesized and demonstrated that Saturn was surrounded by a thin, flat ring system that was nowhere attached to the planet and inclined to its orbit, thus explaining the changing appearances that had so mystified Galileo.

 

Physics and Mechanics 

 

Galileo Galilei: Law of falling bodies

Here’s an image related to Galileo Galilei’s law of falling bodies:

 

Galileo Galilei made significant and groundbreaking contributions to our understanding of the law of falling bodies, fundamentally changing the way motion under gravity was perceived and analyzed. His work challenged the long-held Aristotelian view and established the basis for our modern understanding of free fall.  

Here are the key aspects of Galileo’s work on falling bodies:

• Challenging Aristotle: Aristotle had taught that heavier objects fall faster than lighter ones, with the speed being directly proportional to the weight. Galileo, through both thought experiments and actual (though often idealized) experiments, demonstrated that this was incorrect.  
• The Leaning Tower of Pisa Experiment (Likely a Thought Experiment): While the popular story of Galileo dropping balls of different masses from the Leaning Tower of Pisa to demonstrate that they fall at the same rate is likely more of a thought experiment popularized by his biographers, it effectively illustrates his argument against Aristotle. The core idea is that if a heavier object falls faster, then two lighter objects joined together should fall even faster, which contradicts the idea that they are just a heavier version of the individual lighter objects.
• Experiments with Inclined Planes: Galileo’s primary method of studying falling motion was by using inclined planes. He reasoned that motion down an inclined plane was a “diluted” form of free fall, making it easier to measure distances and times accurately with the technology of his day. By studying the motion of balls rolling down inclined planes of varying angles, he could extrapolate to the case of vertical free fall.
• Discovery of Uniform Acceleration: Through his experiments, Galileo concluded that objects falling under the influence of gravity (ignoring air resistance) accelerate uniformly. This means their velocity increases at a constant rate over time. This was a revolutionary concept.  

Relationship Between Distance, Time, and Acceleration: Galileo mathematically formulated the relationship between the distance fallen (d), the time elapsed (t), and the acceleration due to gravity (g):

d = ½ * g * t²

•  This equation shows that the distance fallen is directly proportional to the square of the time, meaning that in equal intervals of time, a falling object covers increasingly larger distances.
• Independence of Mass (in a Vacuum): Galileo concluded that all objects, regardless of their mass, fall with the same uniform acceleration in a vacuum (i.e., in the absence of air resistance). The difference in falling rates observed in everyday life is primarily due to the effects of air resistance, which affects lighter and less aerodynamic objects more significantly than heavier and more streamlined ones.  
• Publication in Dialogo sopra i due massimi sistemi del mondo (Dialogue Concerning the Two Chief World Systems): Galileo discussed his findings on falling bodies in his famous Dialogue, where he presented arguments against the Aristotelian view and laid out his own conclusions about uniform acceleration and the independence of mass in free fall.

In summary, Galileo’s law of falling bodies established that:

• Objects in free fall accelerate uniformly under the influence of gravity.  
• The distance fallen is proportional to the square of the time elapsed.  
• In the absence of air resistance, all objects fall at the same rate, regardless of their mass.  

His work was a cornerstone of classical mechanics, directly contradicting established dogma and paving the way for Newton’s laws of motion and the law of universal gravitation. Galileo’s emphasis on observation, experimentation, and mathematical formulation was crucial to this scientific revolution.

 

Galileo Galilei: Principle of inertia

Here’s an image related to Galileo Galilei’s principle of inertia:

 

Yes, Galileo Galilei is considered a key figure in developing the principle of inertia. However, he didn’t state it exactly as Isaac Newton later formalized it in his First Law of Motion. Galileo’s work significantly challenged the Aristotelian view of motion and laid much groundwork for Newton’s formulation.  

Here’s how Galileo contributed to the principle of inertia:

• Challenging Aristotelian Physics: Aristotle believed that a constant force was necessary to keep an object moving. He thought that objects naturally came to rest if no force was acting upon them. Galileo’s experiments and thought experiments directly contradicted this idea.  
• Experiments with Inclined Planes: Galileo conducted experiments with balls rolling down inclined planes. He observed that a ball rolling down one plane would roll up another inclined plane to almost the same height it started from, regardless of the angle of the second plane.  
• Extrapolation to Horizontal Motion: Galileo reasoned that if the second plane were perfectly horizontal and frictionless, the ball, having acquired a certain speed, would continue to move along that plane indefinitely without the need for any continuous force to maintain its motion. He concluded that motion, once imparted, tends to continue.  
• Concept of Inertia as a Tendency to Resist Change: While he didn’t use the precise term “inertia” in the way we do today, Galileo understood the concept as an inherent tendency of matter to resist changes in its state of motion. An object at rest tends to stay at rest, and an object in motion tends to stay in motion with the same velocity (speed and direction).  
• Circular Inertia (Initial Idea): Initially, Galileo seemed to believe that this natural, unforced motion was circular. This was partly influenced by the prevailing astronomical idea of celestial bodies moving in circles. He thought that an object moving on a frictionless horizontal plane on the Earth would continue to move in a circle around the Earth’s center.
• Towards Linear Inertia: Later in his work, particularly in his discussions of projectile motion, Galileo’s concept of inertia leaned more towards linear motion in the absence of forces. His analysis of the horizontal component of projectile motion as uniform and unchanging (ignoring air resistance) strongly suggests an understanding of linear inertia.  
• Impact on Newton: Galileo’s ideas about motion and the tendency of objects to maintain their state of motion were highly influential on Isaac Newton. Newton built directly upon Galileo’s work, formalizing the principle of inertia as his First Law of Motion: “Every object persists in its state of being at rest or of moving uniformly straight forward, except insofar as it is compelled to change its state by force impressed.”  

In summary, Galileo Galilei did not explicitly state Newton’s First Law of Motion, but his experiments, observations, and reasoning were crucial in dismantling the Aristotelian view of motion and establishing the fundamental concept of inertia – the tendency of objects to resist changes in their state of motion. His work laid the essential groundwork for Newton’s formalization of this principle.

 

Galileo Galilei: Projectile motions

Here’s an image related to Galileo Galilei’s work on projectile motion:

 

Galileo Galilei made significant and groundbreaking contributions to our understanding of projectile motion, fundamentally changing the way it was analyzed and explained. His work laid the foundation for classical mechanics and had a lasting impact on physics.  

Here are the key aspects of Galileo’s work on projectile motion:

• Breaking Down Motion into Components: Galileo’s most crucial insight was to realize that projectile motion could be analyzed by separating it into two independent components:
  • Horizontal Motion: He recognized that in the absence of air resistance, the horizontal velocity of a projectile remains constant. There is no horizontal force acting on it after it is launched. This is in line with his concept of inertia.  
  • Vertical Motion: He understood that the vertical motion of a projectile is governed by gravity alone, resulting in a constant downward acceleration (the acceleration due to gravity, ‘g’). This motion is identical to that of an object falling freely from rest.
• The Principle of Superposition: Galileo applied the principle of superposition to these independent motions. He argued that the actual trajectory of the projectile is the vector sum of its horizontal and vertical displacements at any given time.  
• Mathematical Description: Using his understanding of constant velocity (for horizontal motion) and constant acceleration (for vertical motion), Galileo was able to derive mathematical equations to describe the trajectory of a projectile:
  • Horizontal Position (x): x = v₀ₓ * t (where v₀ₓ is the initial horizontal velocity and t is time)  
  • Vertical Position (y): y = v₀y * t – ½ * g * t² (where v₀y is the initial vertical velocity, g is the acceleration due to gravity, and t is time)
• Parabolic Trajectory: By combining these equations, Galileo demonstrated that the trajectory of a projectile in a vacuum (ignoring air resistance) is a parabola. This was a significant departure from earlier beliefs, which often involved more complex or non-mathematical descriptions of projectile paths.
• Range, Height, and Time of Flight: Based on his equations, Galileo could theoretically determine the range (horizontal distance traveled), maximum height reached, and time of flight of a projectile given its initial velocity and launch angle.
• Influence of Launch Angle: Galileo understood that the launch angle significantly affects the range and height of a projectile. He theoretically determined that for a given initial speed, the maximum range is achieved at a launch angle of 45 degrees (in a vacuum).
• Experimental Evidence (though idealized): While Galileo’s experiments were often idealized and didn’t fully account for air resistance, he used inclined planes and other setups to study the components of motion and provide evidence supporting his theoretical conclusions. He recognized that air resistance would affect the actual trajectory, especially for objects with low density or high speeds.  
• Publication in Dialogo sopra i due massimi sistemi del mondo (Dialogue Concerning the Two Chief World Systems): Galileo discussed his ideas on projectile motion in his famous Dialogue, published in 1632. Simplicio, representing the Aristotelian view, initially struggles with these concepts, while Salviati, representing Galileo’s views, clearly explains the decomposition of motion and the parabolic trajectory.

In summary, Galileo’s work on projectile motion was revolutionary because he:

• Introduced the concept of analyzing motion into independent horizontal and vertical components.  
• Applied the principle of superposition to determine the trajectory.  
• Mathematically describe the parabolic path of a projectile in a vacuum.  
• Theoretically determined the optimal launch angle for maximum range.

His work laid the essential groundwork for Newton’s laws of motion and the development of classical mechanics, providing a fundamental understanding of how objects move under the influence of gravity.

 

Galileo Galilei: Isochronism of the pendulum

Here’s an image related to Galileo Galilei’s isochronism of the pendulum:

Yes, Galileo Galilei is credited with the discovery of the isochronism of small oscillations of a pendulum. This was a crucial observation that laid the foundation for the development of accurate pendulum clocks.  

Here’s what Galileo observed and concluded:

• Observation in Pisa Cathedral (around 1583): The often-cited story is that while attending mass in the Pisa Cathedral, Galileo observed a lamp swinging back and forth. He supposedly used his pulse to time the swings and noticed that the period of oscillation (the time it took for one complete swing) remained approximately the same regardless of the amplitude (the extent of the swing), as long as the amplitude was small.  
• Formulation of the Principle: Based on this observation and likely further experimentation, Galileo formulated the principle of isochronism for small oscillations of a pendulum. This principle states that for small angles of displacement, the period of a pendulum is largely independent of the amplitude of its swing.  
• Factors Affecting the Period: Galileo also investigated the factors that do affect the period of a pendulum. He determined that the period is primarily dependent on the length of the pendulum (specifically, the distance from the pivot point to the center of mass of the bob) and the acceleration due to gravity. A longer pendulum has a longer period, and a stronger gravitational field results in a shorter period.  

Mathematical Relationship (though not fully derived by Galileo): While Galileo understood the relationships qualitatively, the more precise mathematical relationship for the period of a simple pendulum for small oscillations is given by:

T = 2π√(L/g)

•  Where:
  • T is the period of oscillation.
  • π is pi.
  • L is the length of the pendulum.  
  • g is the acceleration due to gravity.  
• Significance: Galileo’s discovery of isochronism was significant for several reasons:
  • Foundation for Accurate Timekeeping: It provided the fundamental principle for building accurate clocks based on the regular and predictable swing of a pendulum. Christiaan Huygens later built the first practical pendulum clock in the mid-17th century, directly applying Galileo’s findings.  
  • Study of Motion: It contributed to the broader understanding of motion and oscillations in physics.
  • Experimental Method: Galileo’s method of observation and deduction exemplifies the early stages of the scientific method.
• Limitations: It’s important to note that the isochronism of a simple pendulum is only an approximation that holds for small angles of swing. As the amplitude increases, the period also increases slightly. Huygens later addressed this limitation by discovering that a pendulum swinging along a cycloidal arc is perfectly isochronous.  

In conclusion, Galileo Galilei’s observation of the isochronism of small oscillations of a pendulum was a crucial discovery in physics. It revealed a fundamental property of pendular motion and paved the way for the development of accurate timekeeping devices, profoundly impacting navigation, science, and everyday life.

 

Inventions and Improvements

 

Galileo Galilei: Improved Refracting Telescope

Here’s an image related to Galileo Galilei’s improved refracting telescope:

 

Galileo Galilei is famously credited with significantly improving the refracting telescope and using it to make groundbreaking astronomical observations. While he didn’t invent the very first telescope, his enhancements and skillful instrument application revolutionized astronomy.  

Here’s a breakdown of Galileo’s improvements and contributions to the refracting telescope:

• Early Telescopes: The principle of combining lenses to magnify distant objects was likely known before Galileo. Eyeglasses have been around for centuries, and there are accounts of Dutch spectacle makers, such as Hans Lippershey (in 1608), who applied for telescope patents. However, these early telescopes were relatively weak and of limited quality.  
• Galileo’s First Telescope (1609): Upon hearing about these early Dutch “spyglasses” in 1609, Galileo, without having seen one, deduced the principles of their construction through his understanding of optics. He then set about grinding his lenses and building his telescopes. His first telescope had a magnification of only about 3x.  
• Improving Magnification and Quality: Galileo rapidly improved his telescope designs. By the end of 1609, he had constructed instruments with magnifications of around 20x. He achieved this by carefully selecting and grinding lenses with better shapes and longer focal lengths. This resulted in clearer and more magnified images than the early Dutch telescopes.  
• The Galilean Telescope Design: Galileo’s telescopes typically used a convex (converging) lens as the objective lens (to gather light and form a real, inverted image) and a concave (diverging) lens as the eyepiece (to intercept the converging light rays before they formed a real image, creating a virtual, upright, and magnified image for the observer). This design had the advantage of producing an upright image, which was useful for terrestrial observations.  
• Astronomical Observations: The key to Galileo’s impact was not just the improved telescope itself, but his pioneering use of it to make systematic and revolutionary astronomical observations. Starting in late 1609 and continuing in the following years, he made discoveries that fundamentally changed our understanding of the cosmos, including:  
  • The Moon’s Surface: He observed mountains, valleys, and craters on the Moon, showing that it was not a perfect, smooth sphere as previously believed.  
  • The Moons of Jupiter: He discovered the four largest moons of Jupiter (Io, Europa, Ganymede, and Callisto), now known as the Galilean moons, and tracked their orbits around the planet. This provided strong evidence for objects orbiting a body other than Earth, supporting the Copernican model.
  • The Phases of Venus: He observed that Venus goes through a full set of phases, similar to the Moon. This was only possible if Venus orbited the Sun, further supporting the heliocentric view.
  • Sunspots: He observed spots on the Sun and tracked their movement, indicating that the Sun was not a perfect, unchanging celestial body and that it rotated.  
  • The Milky Way’s Structure: He resolved the hazy band of the Milky Way into countless individual stars, showing that it was composed of a vast number of stars too faint to be seen with the naked eye.  
  • Saturn’s Rings (though not fully understood): While he couldn’t resolve them clearly, his observations showed that Saturn had “ears” or appendages, which Huygens later correctly identified as rings.  
• Publication and Advocacy: Galileo published his groundbreaking observations and his arguments for the Copernican system in works like “Sidereus Nuncius” (Starry Messenger) in 1610, which caused a sensation and played a crucial role in the scientific revolution.  

In summary, while Galileo didn’t invent the first telescope, he significantly improved its magnifying power and image quality through careful lens grinding and design. More importantly, he was the first to systematically use the telescope to make profound astronomical observations that provided strong evidence for the heliocentric model and revolutionized our understanding of the solar system and the universe. His work transformed the telescope from a mere novelty into an indispensable tool for scientific discovery.

 

Galileo Galilei: Thermoscope

Here’s an image related to Galileo Galilei’s thermoscope:

Yes, Galileo Galilei is widely credited with the invention of the thermoscope, a device that preceded the modern thermometer. It was a significant early step in the development of instruments for measuring temperature, although it differed considerably from the thermometers we use today.  

Here are the key aspects of Galileo’s thermoscope:

• Likely Invention Around 1596: According to historical sources, including information from temperature instrument specialists, Galileo likely invented the thermoscope around 1596. This aligns with the information from the search snippet provided.
• Principle of Operation: Galileo’s thermoscope consisted of a glass bulb with a long, thin neck. The bulb was heated, and then the open end of the neck was immersed in a liquid, often water or wine. As the air inside the bulb cooled, it contracted, causing the liquid to rise into the neck.  
• Measurement: The rise and fall of the liquid level in the neck of the tube indicated changes in temperature. A higher liquid level corresponded to a lower temperature (because the air in the bulb had contracted more), and a lower liquid level indicated a higher temperature.
• Key Differences from Modern Thermometers:
  • Not Sealed: Galileo’s thermoscope was not sealed, meaning the air pressure inside the bulb could be affected by changes in atmospheric pressure, not just temperature. This made it susceptible to inaccuracies.
  • Arbitrary Scale: It lacked a standardized temperature scale. Different thermoscopes would have different dimensions and use other liquids, making it challenging to compare readings between instruments.  
  • Qualitative Measurement: It provided a qualitative indication of relative hotness or coldness rather than a precise quantitative measurement with fixed units like Celsius or Fahrenheit.
• Significance: Despite its limitations, Galileo’s thermoscope was a crucial early step in the history of thermometry. It demonstrated the principle that changes in temperature cause changes in the volume of a gas. By addressing its shortcomings (sealing the instrument and establishing a temperature scale), it paved the way for later scientists to develop more accurate and standardized thermometers.  
• Santorio Santorio’s Contribution: As the search snippet also mentions, Santorio Santorio, a colleague of Galileo, is credited with being the first to put a numerical scale on a thermoscope around 1612, effectively creating the first rudimentary thermometer. However, Santorio’s instruments were still air-based and suffered from the same atmospheric pressure issues as Galileo’s.  

In summary, Galileo Galilei invented the thermoscope around 1596. It was an open-air device that showed changes in temperature through the expansion and contraction of air, affecting the level of a liquid in a tube. While not a precise thermometer in the modern sense, it was a foundational invention that demonstrated the basic principles of thermal expansion and laid the groundwork for future developments in temperature measurement.

 

Galileo Galilei: Military and geometric compass

Here’s an image related to Galileo Galilei’s military and geometric compass:

 

Galileo Galilei was indeed the inventor and marketer of a device known as the military compass or geometric and military compass. This significant practical invention showcased his ingenuity beyond pure astronomical observations and theoretical physics.  

Here are the key aspects of Galileo’s military compass:

• Invention and Development: Galileo likely began developing his compass around the 1590s while a professor at the University of Padua. He refined and improved the design over several years.
• Description and Functionality: Galileo’s compass was a sophisticated instrument made of brass. It consisted of two arms connected by a hinge, similar to a drawing compass, but with numerous scales and markings inscribed on them. It was designed to perform a wide range of practical calculations for both military and civil applications, including:  
  • Military Uses:
    • Calculating the elevation needed for aiming cannons based on the range and caliber of the shot. This was a crucial application for the military of the time.
    • Determining the quantity of gunpowder required for different types of artillery.
    • Laying out fortifications and surveying terrain.
    • Measuring distances and heights indirectly.
  • Geometric and Civil Uses:
    • Calculating interest rates and currency conversions.
    • Determining proportions for mixtures of metals.
    • Calculating areas of geometric figures.
    • Performing trigonometric calculations.
    • Extracting square and cube roots.
• Marketing and Sales: Galileo was not just an inventor but also a shrewd marketer. He recognized the practical value of his compass, particularly for the military. He established a workshop in his house where these compasses were manufactured and sold to wealthy individuals, military officers, and even rulers. He also employed assistants to demonstrate and promote the instrument.
• Instruction Manual: To further help people adopt and use his invention, Galileo wrote a detailed instruction manual titled “Le operazioni del compasso geometrico et militare” (Operations of the Geometric and Military Compass), first published in 1606. This manual clearly explained the various scales and how to use the compass for different calculations, making it accessible to a wider audience.  
• Controversies and Disputes: Galileo’s compass was not without its controversies. Some of its features were accused of plagiarism. However, Galileo vigorously defended his invention and his priority.  
• Significance: Galileo’s military compass was a successful commercial venture and a testament to his ability to apply his mathematical and geometric knowledge to solve practical problems. It provided a valuable tool for the military and other professions, demonstrating the utility of mathematics in real-world applications. While his astronomical work is more widely remembered today, the military compass was an important aspect of his career and contributed to his income and influence.  

In conclusion, the military and geometric compass was a significant invention by Galileo Galilei. It showcased his practical skills and his ability to translate theoretical knowledge into a useful and marketable device for military and civil purposes.

 

Johannes Kepler (1571–1630)

Johannes Kepler

(Wiki Image By August Köhler [1] – Kepler-Museum in Weil der Stadt, Public Domain, https://commons.wikimedia.org/w/index.php?curid=9406242) 

Johannes Kepler Quotes

Johannes Kepler, a key figure in the 17th-century scientific revolution, left behind many writings that reveal his profound thoughts on astronomy, mathematics, God, and the harmonious nature of the universe. Here is a selection of insightful quotes attributed to him:

1. “The chief aim of all investigations of the external world should be to discover the rational order and harmony which has been imposed on it by God and which He revealed to us in the language of mathematics.”  
2. “Geometry is one and eternal shining in the mind of God. That share in it accorded to humans is one of the reasons that humanity is the image of God.”  
3. “I much prefer the sharpest criticism of a single intelligent man to the thoughtless approval of the masses.”
4. “The diversity of the phenomena of nature is so great, and the treasures hidden in the heavens so rich, precisely in order that the human mind shall never be lacking in fresh nourishment.”  
5. “Truth is the daughter of time, and I feel no shame in being her midwife.”
6. “My aim is to show that the celestial machine is to be likened not to a divine organism but rather to a clockwork.”
7. “I used to measure the heavens, now I measure the shadows of Earth. Although my mind was sky-bound, the shadow of my body lies here.” (An epitaph Kepler wrote for himself).  
8. “O telescope, instrument of much knowledge, more precious than any sceptre!”
9. “The ways by which men arrive at knowledge of the celestial things are hardly less wonderful than the nature of these things themselves.”  
10. “I feel carried away and possessed by an unutterable rapture over the divine spectacle of the heavenly harmony.” (Often associated with his work Harmonices Mundi).
11. “Let [my book] await its reader for a hundred years, if God himself has stood ready for six thousand years for one to study his work.” (From the preface to Harmonices Mundi, regarding his belief in the eventual acceptance of his work).
12. “Nature uses as little as possible of anything.”

These quotes illustrate Kepler’s deep belief in a mathematically ordered and divinely created cosmos, his dedication to empirical investigation, and his profound sense of wonder at the universe.

 

Johannes Kepler YouTube Video

Johannes Kepler: God’s Mathematician

Kepler

Kepler: The Man Who Dreamed The Universe (part 1)

 

Johannes Kepler History

As a child, Kepler witnessed the Great Comet of 1577, which attracted the attention of astronomers across Europe.

(Wiki Image By Jiřrí Jakubuv Dačický – Zentralbibliothek Zürich, Public Domain, https://commons.wikimedia.org/w/index.php?curid=70591808) 

 

Johannes Kepler (December 27, 1571 – November 15, 1630) was a pivotal German astronomer, mathematician, and astrologer whose work fundamentally altered humanity’s understanding of the cosmos and laid crucial groundwork for Isaac Newton’s theory of universal gravitation. He is best known for his three laws of planetary motion.  

Here’s an overview of his history:

1. Early Life and Education (1571-1594):
   • Born in Weil der Stadt, in the Holy Roman Empire (now Germany), Kepler experienced a difficult childhood marked by family instability and illness (smallpox left him with weakened eyesight and crippled hands).  
   • Despite these challenges, he displayed exceptional mathematical brilliance from a young age.  
   • He received a scholarship to the University of Tübingen, where he studied theology, philosophy, and mathematics. His astronomy professor, Michael Maestlin, introduced him to Nicolaus Copernicus’s heliocentric (Sun-centered) theories. Kepler became a strong advocate for the Copernican system.  
2. Graz and Mysterium Cosmographicum (1594-1600):
   • In 1594, Kepler abandoned his theological studies to accept a position as a teacher of mathematics and astronomy in Graz, Austria.  
   • In 1596, he published his first major astronomical work, Mysterium Cosmographicum (The Cosmographic Mystery). In this book, he defended the Copernican system and proposed a model of the solar system where the distances of the planets from the Sun were related to nested Platonic solids. While this specific model was incorrect, the work showcased his mathematical skill and commitment to finding a divine, harmonious order in the universe. It also brought him to the attention of other astronomers, including Tycho Brahe.  
3. Prague, Tycho Brahe, and Imperial Mathematician (1600-1612):  
   • Facing religious persecution as a Lutheran in Catholic Graz, Kepler moved to Prague in 1600 to work as an assistant to Tycho Brahe, the renowned Danish astronomer who was then the Imperial Mathematician to Emperor Rudolf II.  
   • Tycho Brahe had amassed the most extensive and accurate naked-eye astronomical observations of his time, particularly of planetary positions.  
   • After Tycho’s sudden death in 1601, Kepler succeeded him as Imperial Mathematician and, crucially, gained access to Tycho’s invaluable observational data, especially for the planet Mars.  
4. Laws of Planetary Motion:
   • Kepler’s most enduring legacy is his discovery of the three laws of planetary motion, derived from his meticulous analysis of Tycho Brahe’s observations:
     • First Law (1609, in Astronomia Nova): Planets move in elliptical orbits with the Sun at one of the two foci of the ellipse. This broke decisively with the ancient and Copernican tradition of perfect circular orbits.  
     • Second Law (1609, in Astronomia Nova): A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. This implies that planets move faster when they are closer to the Sun and slower when they are farther away.  
     • Third Law (1619, in Harmonices Mundi): The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit (T2</1>∝a3). This law relates the orbital periods of different planets to their distances from the Sun.  
   • These laws revolutionized astronomy, providing a precise mathematical description of planetary motion within a heliocentric system.
5. Contributions to Optics (1604, 1611):
   • Kepler made significant contributions to the field of optics. In Astronomiae Pars Optica (The Optical Part of Astronomy, 1604), he explored the workings of the human eye, refraction, and the pinhole camera.  
   • In Dioptrice (1611), he described the principles of the telescope using two convex lenses (the “Keplerian telescope”), which became the dominant design for astronomical refracting telescopes.  
6. Later Career, Rudolphine Tables, and Somnium (1612-1630):
   • After leaving Prague, Kepler worked as a district mathematician in Linz, Austria (1612-1626).  
   • He published the Epitome Astronomiae Copernicanae (Epitome of Copernican Astronomy, published in parts between 1618 and 1621), which became an influential textbook defending and explaining heliocentric astronomy based on his laws.  
   • In 1627, he finally published the Rudolphine Tables, astronomical tables based on Tycho Brahe’s observations and his own laws. These tables were far more accurate than any previous ones and greatly facilitated the acceptance of the Copernican system.  
   • He also wrote Somnium (The Dream), a novel-like work published posthumously in 1634, which describes an imaginary trip to the Moon and is considered by some to be an early work of science fiction.  
7. Personal Life and Challenges:
   • Kepler’s life was marked by personal hardships, including religious persecution (he was forced to move several times), financial instability, the death of his first wife and several of his children, and the emotional turmoil of defending his mother against accusations of witchcraft.  
   • He also engaged in astrological work, a common practice for astronomers of his era, and sought to find harmonies and divine design in the cosmos, as explored in works like Harmonices Mundi.  
8. Death and Legacy:
   • Johannes Kepler died in Regensburg, Germany, on November 15, 1630, while on a journey to collect an old debt.  
   • His work was a cornerstone of the Scientific Revolution. His laws of planetary motion transformed astronomy and provided the essential foundation upon which Isaac Newton later built his theory of universal gravitation. Kepler is remembered as one of history’s most important and innovative scientists.

 

Johannes Kepler’s Discoveries Table

Okay, here is a table summarizing Johannes Kepler’s major scientific discoveries and contributions:

Discovery/Contribution	Significance/Details/Associated Work
Astronomy / Celestial Mechanics
First Law of Planetary Motion	Planets move in elliptical orbits with the Sun at one focus (Published in Astronomia Nova, 1609), which breaks from the ancient and Copernican tradition of perfect circular orbits.
Second Law of Planetary Motion	A line joining a planet and the Sun sweeps out equal areas during equal intervals of time.  (Published in Astronomia Nova, 1609). This means planets move faster when closer to the Sun.
Third Law of Planetary Motion (Harmonic Law)	The square of a planet’s orbital period is proportional to the cube of the semi-major axis of its orbit (T2∝a3). (Published in Harmonices Mundi, 1619). Relates orbital periods to distances.
Rudolphine Tables	Astronomical tables, based on Tycho Brahe’s observations and Kepler’s laws, were published in 1627. They were far more accurate than previous tables and greatly aided navigation and astronomy.
Kepler’s Supernova (SN 1604)	Observed and provided a detailed account of a supernova in 1604 (De Stella Nova). This “new star” challenged the Aristotelian idea of unchanging heavens.
Study of Mars’s Orbit	His meticulous and arduous analysis of Tycho Brahe’s observations of Mars was crucial for deriving his first two laws of planetary motion.
Mysterium Cosmographicum	(1596) His first major astronomical work, defending Copernicanism and proposing a model of the solar system based on nested Platonic solids (later superseded by his laws).
Epitome Astronomiae Copernicanae	(1618-1621) An influential textbook that systematically presented heliocentric astronomy based on his new elliptical laws.
Somnium (The Dream)	A posthumously published (1634) work describing an imaginary trip to the Moon, considered an early work of science fiction and a treatise on lunar astronomy.
Optics
Explanation of Vision	Correctly explained, the eye forms an inverted image on the retina. (Astronomiae Pars Optica, 1604).
Principles of the Pinhole Camera	Explained the image formation in a pinhole camera. (Astronomiae Pars Optica, 1604).
Law of Refraction (Approximate)	Formulated an approximate law for light refraction.
Keplerian Telescope Design	Described a telescope design using two convex lenses (Dioptrice, 1611), which allowed for a wider field of view and higher magnification than Galileo’s design, becoming standard for astronomy.
Depth Perception (Binocular Vision)	Explained the use of two eyes for depth perception.
Mathematics
Work on Logarithms	Promoted the use of logarithms (invented by Napier) in astronomical calculations and published his own logarithm tables.
Infinitesimal Methods	Used methods that were precursors to integral calculus, particularly in calculating areas and volumes (e.g., in Stereometria Doliorum Vinariorum for wine barrel volumes).
Geometry of Solids / Sphere Packing	Investigated the geometry of Platonic and Archimedean solids; made conjectures on the densest way to pack spheres (Kepler Conjecture). Discovered two new regular polyhedra (Kepler-Poinsot polyhedra, though Poinsot later rediscovered/completed them).

Export to Sheets

 

Johannes Kepler’s work was foundational to the Scientific Revolution, providing the mathematical underpinnings for a new understanding of the cosmos.

 

Astronomy / Celestial Mechanics 

Johannes Kepler: First law of planetary motion

Here’s an image related to Johannes Kepler’s first law of planetary motion:

Johannes Kepler’s First Law of Planetary Motion, often called the Law of Ellipses, describes the shape of the orbits of planets around the Sun. He published this groundbreaking law, along with his second law, in his seminal work Astronomia Nova (A New Astronomy) in 1609.  

Here’s a breakdown of the law and its significance:

1. Statement of the Law:
   • Kepler’s First Law states: “The orbit of every planet is an ellipse with the Sun at one of the two foci.”  
2. Explanation and Meaning:
   • Ellipse: An ellipse is an oval shape that can be defined by two special points called foci (singular: focus). For any point on the ellipse, the sum of the distances to the two foci is constant.  
   • Sun at a Focus: This law means that planets do not orbit the Sun in perfect circles, as had been believed for over two millennia (from ancient Greek astronomers like Ptolemy through to Copernicus). Instead, their paths are elliptical, and the Sun is not at the center of the ellipse but rather at one of its two focal points. The other focal point is empty space.  
   • Varying Distance: A consequence of this elliptical path with the Sun at a focus is that a planet’s distance from the Sun varies throughout its orbit. The point where a planet is closest to the Sun is called the perihelion, and the point where it is farthest is called the aphelion.  
3. Historical Context and Revolutionary Nature:
   • This law was a radical departure from a deeply entrenched astronomical tradition that spanned over 2,000 years. The circle was considered the perfect geometric shape, and thus, celestial motions were assumed to be perfectly circular or combinations of circles (like epicycles and deferents in the Ptolemaic system, or even in Copernicus’s initial heliocentric model).  
   • Kepler’s discovery that orbits were elliptical was based on his incredibly detailed and persistent analysis of Tycho Brahe’s precise observational data for the planet Mars. Kepler struggled for years to fit Mars’s observed positions to various circular and oval models before finally realizing that an ellipse provided the correct solution.  
4. Significance:
   • Accurate Geometric Model: It provided the first accurate geometric description of how planets move around the Sun, significantly improving the predictive power of astronomical models.  
   • Simplification of the Solar System: By replacing complex systems of circles-on-circles (epicycles) with a single ellipse per planet, Kepler’s law offered a much simpler and more elegant model of the solar system.
   • Foundation for Physical Explanation: It was a crucial step towards a physical understanding of planetary motion. The non-uniform, non-circular motion demanded a new physical explanation, which Isaac Newton later provided with his law of universal gravitation. Newton showed that an inverse-square law of gravity naturally produces elliptical orbits as described by Kepler.  
   • Emphasis on Empirical Data: Kepler’s unwavering commitment to making theory fit Tycho Brahe’s highly accurate observational data, even when it meant abandoning long-cherished assumptions about circular motion, was a hallmark of the emerging scientific method.

Kepler’s First Law fundamentally changed our understanding of the architecture of the solar system and was a cornerstone of the Scientific Revolution.

 

Johannes Kepler: Second law of planetary motion

Here’s an image related to Johannes Kepler’s second law of planetary motion:

Johannes Kepler’s Second Law of Planetary Motion, often called the Law of Equal Areas, describes the speed at which a planet moves as it orbits the Sun. He published this law and his first law in his groundbreaking work Astronomia Nova (A New Astronomy) in 1609.  

Here’s a breakdown of the law and its significance:

1. Statement of the Law:
   • Kepler’s Second Law states: “A line joining a planet and the Sun sweeps out equal areas during equal intervals of time.”
2. Explanation and Meaning:
   • Imagine an imaginary line connecting the center of the Sun to the center of a planet. As the planet moves along its elliptical orbit, this line “sweeps out” an area in the plane of the orbit.  
   • The law means that if you measure the area swept out by this line over a certain period (e.g., 30 days) when the planet is close to the Sun, and then measure the area swept out over the same period when the planet is far from the Sun, these two areas will be equal.
   • Key Implication (Varying Orbital Speed): For these areas to be equal, the planet must be moving faster when it is closer to the Sun (at its perihelion) and slower when it is farther from the Sun (at its aphelion). This was a radical departure from the ancient Greek astronomical tradition, which held that celestial bodies moved with uniform circular motion.  
3. Context of Discovery:
   • Kepler derived this law, along with his first law (that planets move in elliptical orbits), through his painstaking mathematical analysis of the highly accurate observational data of Mars’s orbit, collected by Tycho Brahe.
   • He was trying to understand why Mars’s observed positions did not fit models based on perfect circles and uniform speeds. The law of equal areas was a geometric solution he found to describe the planet’s varying speed.  
4. Significance:
   • Overturned Uniform Motion: It decisively overturned the long-held axiom of uniform circular motion for planets, which had been a cornerstone of astronomy since antiquity and was still retained by Copernicus.  
   • Described Variable Speed: It provided a precise, quantitative way to describe how a planet’s speed changes throughout its orbit.
   • Pointed to a Central Force: The fact that planets speed up as they approach the Sun and slow down as they recede strongly suggested that the Sun exerted some kind of influence or force that governed their motion, although Kepler did not fully understand the nature of this force (which Newton later identified as gravity).
   • Foundation for Newton: Kepler’s Second Law (along with his other two laws) was a critical piece of empirical evidence that Isaac Newton used to develop his law of universal gravitation and his laws of motion. The law of equal areas is a direct consequence of the conservation of angular momentum, which applies to any object moving under the influence of a central force (like gravity).  

Kepler’s Second Law was a crucial step in accurately describing the true motions of the planets and moving astronomy towards a physically based understanding of the solar system.

 

Johannes Kepler: Third law of planetary motion (Harmonic Law)

Here’s an image related to Johannes Kepler’s third law of planetary motion (Harmonic Law):

Johannes Kepler’s Third Law of Planetary Motion, often referred to as the Harmonic Law, establishes a mathematical relationship between a planet’s orbital period and its average distance from the Sun. He published this law in his 1619 work, Harmonices Mundi (The Harmony of the Worlds).  

Here’s a breakdown of the law and its significance:

1. Statement of the Law:
   • Kepler’s Third Law states: “The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.”  
   • Mathematically, this is expressed as: T2∝a3 Where:
     • T is the orbital period of the planet (the time it takes for the planet to complete one orbit around the Sun).  
     • a is the semi-major axis of the planet’s elliptical orbit (which can be thought of as its average distance from the Sun).  
   • This means that if you take the orbital period of any planet, square it, and then divide by the cube of its semi-major axis, you will get (approximately) the same constant value for all planets orbiting the same central body (in this case, the Sun). T2/a3=k (where k is a constant for all planets orbiting the Sun)  
2. Context of Discovery:
   • Kepler discovered this law after publishing his first two laws (which described the elliptical shape of orbits and the law of equal areas) in Astronomia Nova (1609).  
   • The Third Law was the culmination of his long and arduous search for a “harmony” in the cosmos – a divine, mathematical order underlying the structure and motions of the solar system. He was deeply influenced by Pythagorean ideas of musical harmony and geometric perfection. He found this law on May 15, 1618, after many years of calculation and searching for such a relationship.
3. Explanation and Meaning:
   • The law implies that planets farther from the Sun not only have longer orbital paths but also move more slowly in their orbits. The relationship is not linear; the increase in orbital period is much more dramatic than the increase in distance.  
   • For example, if Planet B is four times as far from the Sun as Planet A, then Planet B’s orbital period will be eight times that of Planet A.
4. Significance:
   • Unified Solar System: Unlike Kepler’s first two laws, which describe the motion of an individual planet, the Third Law establishes a fundamental relationship between the different planets orbiting the Sun. It showed a common mathematical principle governing the entire solar system.
   • Predictive Power: It allowed astronomers to calculate the relative distance of a planet from the Sun if its orbital period was known, or vice versa, given one planet’s period and distance as a reference.
   • Foundation for Newton’s Law of Gravitation: Kepler’s Third Law was absolutely crucial for Isaac Newton in formulating his law of universal gravitation. Newton was able to show that an inverse-square law of gravitational force would produce precisely the relationship Kepler had discovered observationally (and mathematically from Tycho Brahe’s data).  
   • Universality: While discovered for the planets of our solar system, the law is universal for any system of bodies orbiting a central mass due to gravity (e.g., moons orbiting a planet, exoplanets orbiting other stars), provided the mass of the orbiting bodies is much smaller than the central body.

Kepler’s Third Law was a profound discovery, transforming the understanding of the solar system from a collection of individual planetary paths into an interconnected, mathematically harmonious system, and it played a vital role in the development of classical physics.

 

Johannes Kepler: Rudolphine Tables

Here’s an image related to Johannes Kepler’s Rudolphine Tables:

The Rudolphine Tables (Tabulae Rudolphinae) were an exceptionally important and influential star catalog and planetary tables published by Johannes Kepler in 1627. They are considered the first truly scientific and accurate set of astronomical tables, significantly improving upon previous attempts and playing a crucial role in the advancement of astronomy.

Here’s why the Rudolphine Tables were so significant:

• Based on Tycho Brahe’s Precise Observations: The tables were primarily based on the decades of meticulous and highly accurate astronomical observations made by Tycho Brahe. Brahe’s data was the most comprehensive and precise of its time, unmarred by the limitations of earlier instruments and observational techniques.
• Calculated Using Kepler’s Laws: Kepler painstakingly used his newly discovered laws of planetary motion to calculate the positions of the planets for the Rudolphine Tables. This was a radical departure from previous tables that relied on circular orbits and complex systems of epicycles and deferents, which inherently introduced inaccuracies. By employing elliptical orbits and his laws of equal areas and the harmonic law, Kepler’s calculations were far more accurate in predicting planetary positions.
• Comprehensive Star Catalog: In addition to the planetary tables, the Rudolphine Tables included a catalog of over 1,000 stars, with their positions meticulously determined based on Brahe’s and earlier observations. This star catalog was also significantly more accurate and comprehensive than previous catalogs.
• Foundation for Future Astronomy: The accuracy and reliability of the Rudolphine Tables made them an indispensable tool for astronomers for over a century. They were used to:
  • Predict planetary positions with unprecedented accuracy.
  • Improve navigation.
  • Test and refine astronomical theories, including Newton’s law of universal gravitation.
  • Serve as a standard reference for celestial coordinates.
• Long and Difficult Compilation: The creation of the Rudolphine Tables was a long and arduous process. Kepler inherited Brahe’s data after Brahe’s death in 1601 and spent over two decades performing the complex calculations, often facing financial difficulties and interruptions. The final publication was a testament to Kepler’s dedication and perseverance.
• Named After Emperor Rudolf II: The tables were named in honor of Emperor Rudolf II, Kepler’s patron, although the Emperor’s support was often inconsistent.

In summary, the Rudolphine Tables were a landmark achievement in astronomy. By combining Tycho Brahe’s unparalleled observational data with Johannes Kepler’s revolutionary laws of planetary motion, they provided the most accurate and comprehensive astronomical tables of their time, serving as a cornerstone for future astronomical research and solidifying the heliocentric view of the solar system.

 

Johannes Kepler: Kepler’s Supernova (SN 1604)

Here’s an image related to Johannes Kepler’s Supernova (SN 1604):

Yes, Johannes Kepler played a significant role in the observation and study of the supernova that appeared in 1604, now famously known as Kepler’s Supernova or SN 1604.  

Here’s how Kepler was involved:

• Discovery and Observation: The supernova was first widely observed on October 9, 1604. Kepler, who was working as the imperial mathematician for Emperor Rudolf II in Prague at the time, began his own detailed observations of the celestial event shortly thereafter.  
• “De Stella Nova in Pede Serpentarii” (On the New Star in the Foot of the Serpent Bearer): Kepler meticulously documented his observations of the supernova in his book De Stella Nova in Pede Serpentarii, et qui tribus superioribus annis conspecta fuit in Cygno (On the New Star in the Foot of the Serpent Bearer, and which was visible in the three preceding years in Cygnus), published in 1606. This book is a primary source for our understanding of SN 1604.  
• Detailed Record Keeping: Kepler kept careful records of the supernova’s position, brightness, and changes in its luminosity over time. His observations were crucial because they provided a systematic and relatively accurate dataset for future study.  
• Analysis and Interpretation: In his book, Kepler analyzed the supernova from various perspectives:
  • Astronomical: He meticulously tracked its movement (or lack thereof, demonstrating its stellar nature rather than being atmospheric). He also tried to determine its distance, though without modern tools, this was speculative.
  • Astrological: As was common at the time, Kepler also explored the astrological significance of the “new star,” linking it to terrestrial events. However, his primary focus was on its astronomical nature.
  • Philosophical/Cosmological: The appearance of a new star challenged the Aristotelian view of an unchanging celestial sphere beyond the Moon. Kepler’s observations and his discussion of the supernova contributed to the growing acceptance of a more dynamic and evolving cosmos.  
• Naming the Supernova: While the supernova wasn’t officially named “Kepler’s Supernova” during his lifetime, his extensive study and prominent publication about it led to this lasting association.
• Last Naked-Eye Supernova in the Milky Way: SN 1604 was the last supernova in our Milky Way galaxy to be unequivocally observed with the naked eye. The next confirmed Milky Way supernova (Cassiopeia A’s light reached Earth around 1680) was only visible with telescopes, as it was heavily obscured by dust. This makes Kepler’s observations of SN 1604 particularly valuable.  

In summary, Johannes Kepler made a significant contribution to our understanding of the supernova of 1604 through his detailed observations, systematic record-keeping, and comprehensive analysis published in his book De Stella Nova. His work remains a crucial historical record of this important astronomical event, which challenged prevailing cosmological views and was the last naked-eye supernova seen in the Milky Way.

 

Johannes Kepler: Study of Mars’s orbit

Here’s an image related to Johannes Kepler’s study of Mars’s orbit:

Johannes Kepler’s study of Mars’s orbit was pivotal to his groundbreaking discoveries and the formulation of his laws of planetary motion. His meticulous and persistent analysis of Tycho Brahe’s incredibly precise observations of Mars ultimately led him to abandon the long-held belief in circular orbits and establish that planets move in elliptical orbits.  

Here’s a breakdown of Kepler’s crucial work on Mars’s orbit:

• The Problem with Circular Orbits: When Kepler began working with Tycho Brahe’s data, the prevailing astronomical models, including Copernicus’s, still relied on combinations of perfect circles (epicycles and deferents) to describe planetary motion. However, Brahe’s highly accurate observations, particularly of Mars, consistently deviated from the predictions of these circular models.
• Kepler’s Initial Attempts: Kepler initially tried to fit Mars’s orbit using various combinations of circles, as was the standard practice. He spent years wrestling with the data, attempting to reconcile the observations with circular paths. However, he found that no matter how he adjusted the epicycles and deferents, he couldn’t accurately match Brahe’s measurements. The discrepancies, though small, were persistent and exceeded the expected observational error.
• The Crucial Eight Minutes of Arc: One particularly stubborn discrepancy was about eight minutes of arc in Mars’s position. This seemingly small difference was crucial for Kepler. He famously declared that “out of these eight minutes [of arc] we will construct a new astronomy.” This highlights his commitment to the accuracy of the data and his willingness to challenge fundamental assumptions based on even minor deviations.  
• Abandoning the Circle: The persistent failure of circular models to explain Mars’s orbit forced Kepler to consider alternative geometric shapes. This was a radical departure from centuries of astronomical tradition that held the circle as the most perfect and natural form for celestial motion.  
• The Discovery of the Ellipse: After years of intense calculation and analysis, Kepler finally realized that the orbit of Mars could be accurately described by an ellipse, with the Sun located at one of the two foci of the ellipse. This was his First Law of Planetary Motion.  
• The Law of Equal Areas: In his struggle with Mars’s varying speed along its orbit (which couldn’t be explained by uniform circular motion), Kepler also discovered his Second Law of Planetary Motion, the law of equal areas. He found that a line joining Mars and the Sun sweeps out equal areas during equal intervals of time. This meant that Mars moves faster when it is closer to the Sun and slower when it is farther away.  
• Publication in Astronomia Nova (1609): Kepler published his first two laws of planetary motion, derived from his detailed study of Mars’s orbit, in his groundbreaking book Astronomia Nova (New Astronomy) in 1609. This work marked a pivotal shift in astronomy, moving away from purely geometric models to a more physical and mathematically accurate description of celestial motion.  
• Foundation for the Third Law: Kepler’s work on Mars’ orbit, particularly the determination of its elliptical shape and varying speed, laid the groundwork for his later discovery of the Third Law of Planetary Motion (the Harmonic Law), which relates a planet’s orbital period to its orbital size.  

In conclusion, Johannes Kepler’s meticulous and persistent study of the orbit of Mars, driven by his commitment to accurately matching Tycho Brahe’s precise observations, was the key to his revolutionary discoveries. The failure of circular models to explain Mars’s motion led him to the groundbreaking realization that planets move in elliptical orbits and that their speed varies predictably along that orbit, as described by his first two laws of planetary motion. This work on Mars fundamentally changed our understanding of the solar system and paved the way for Newton’s law of universal gravitation.

 

Johannes Kepler: Mysterium Cosmographicum

“Mysterium Cosmographicum” (The Cosmographic Mystery), published in 1596, was Johannes Kepler’s first major published work. It holds significant historical importance as it represents his initial attempt to find a geometric structure underlying the arrangement and spacing of the planetary orbits known at the time (Mercury, Venus, Earth, Mars, Jupiter, and Saturn).  

Here’s why Mysterium Cosmographicum is notable:

• Early Support for Copernicanism: Although Kepler later made significant modifications to Copernicus’s model, Mysterium Cosmographicum was a strong early endorsement of the heliocentric (Sun-centered) view of the solar system. This was a bold stance at a time when the geocentric (Earth-centered) model still held significant sway.
• The Polyhedral Model: Kepler’s central idea in this work was that the spacings of the planetary orbits were determined by the five Platonic solids (tetrahedron, cube, octahedron, dodecahedron, and icosahedron) nested within a series of concentric spheres. He proposed that God had used these perfect geometric solids as a blueprint for the cosmos.  
  • His model involved a specific ordering of the Platonic solids, with a sphere representing each planet’s orbit. The ratios of the spheres’ radii were supposed to correspond to the relative sizes of the inscribed and circumscribed spheres of the nested Platonic solids.  
• Attempt at a Physical Explanation: Kepler wasn’t just interested in a mathematical description; he sought a physical cause for the observed structure of the solar system. His polyhedral model was his initial attempt to find a fundamental, geometric reason for why there were six planets (as known then) and why their orbits were spaced as they were.  
• Blend of Mysticism and Science: The Mysterium Cosmographicum reflects a blend of mystical and mathematical thinking, characteristic of some intellectual currents of the time. Kepler’s deep belief in the harmony and mathematical order of the universe drove him to seek such elegant geometric explanations.  
• Limited Success but Significant Influence: While Kepler’s polyhedral model ultimately did not accurately predict the planetary distances (as his later work with elliptical orbits showed), the Mysterium Cosmographicum was still a highly influential work.
  • It brought Kepler to the attention of prominent astronomers, including Tycho Brahe, who was impressed by Kepler’s mathematical abilities and invited him to collaborate in Prague. This collaboration was crucial for Kepler’s later groundbreaking discoveries of his laws of planetary motion.  
  • It demonstrated Kepler’s commitment to a physical astronomy, seeking underlying causes rather than just mathematical descriptions.  
  • It played a role in the ongoing debate about the structure of the solar system and helped to solidify Kepler’s reputation as a talented and original thinker.

In summary, Johannes Kepler’s Mysterium Cosmographicum was his first major work, notable for its early and enthusiastic support of Copernicanism and its bold attempt to explain the spacing of planetary orbits using the five Platonic solids. Although the specific model proved incorrect, the book was a crucial step in Kepler’s career, leading to his collaboration with Tycho Brahe and setting the stage for his later, more accurate laws of planetary motion. It also exemplifies his lifelong quest to find a harmonious and mathematical order in the cosmos.

 

Johannes Kepler: Epitome Astronomiae Copernicanea

“Epitome Astronomiae Copernicanae” (Epitome of Copernican Astronomy) is a highly significant and influential work by Johannes Kepler. It was published in installments between 1618 and 1621.  

Here’s why it’s so important:

• Systematic Presentation of Heliocentric Astronomy: The Epitome served as a comprehensive and systematic textbook of Copernican heliocentric astronomy. Unlike Kepler’s earlier, more dense and sometimes esoteric works like Astronomia Nova and Harmonices Mundi, the Epitome aimed to be a clear and organized exposition of the heliocentric model as Kepler understood it.  
• Integration of Kepler’s Laws: Crucially, the Epitome was the first published work to present all three of Kepler’s laws of planetary motion together in a unified framework. These laws, derived from his painstaking analysis of Tycho Brahe’s observations, provided a far more accurate and physically grounded model of the solar system than the earlier circular models of Copernicus and Ptolemy. The three laws are:
  • The Law of Ellipses: The orbit of each planet is an ellipse with the Sun at one focus.  
  • The Law of Equal Areas: A line joining a planet and the Sun sweeps out equal areas during equal intervals of time.  
  • The Harmonic Law: The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit (T² ∝ a³).  
• Physical Explanations: Beyond just describing the mathematical relationships of planetary motion, Kepler attempted to provide physical explanations for why the planets moved as they did. He speculated about a “motive soul” or a physical force emanating from the Sun that drove the planets. While his physical ideas were not entirely correct by modern standards, they represented an important step towards a more mechanistic understanding of the cosmos.
• Influence and Spread of Copernicanism: The Epitome was widely read and became a key text for disseminating and popularizing the Copernican heliocentric view across Europe. Its clear and organized structure made the complex ideas more accessible to a broader audience of astronomers and natural philosophers.  
• Defense of Heliocentrism: Kepler robustly defended the heliocentric model against the geocentric (Earth-centered) view, providing arguments based on observational evidence and physical reasoning.  
• Structure and Content: The Epitome was structured in the form of questions and answers, making it suitable for teaching. It covered a wide range of astronomical topics, including:  
  • The arguments for and against the heliocentric system.
  • The properties of planetary orbits according to Kepler’s laws.  
  • Lunar theory.
  • Stellar parallax (though not yet observed).
  • Cosmology.
• Controversy and Censorship: Despite its scientific importance, the Epitome faced opposition, particularly from the Catholic Church. In 1633, it was placed on the Index Librorum Prohibitorum (List of Prohibited Books) due to its advocacy of the heliocentric system.  

In summary, Johannes Kepler’s “Epitome Astronomiae Copernicanae” was a landmark work that provided the first comprehensive and systematic exposition of heliocentric astronomy, incorporating his revolutionary laws of planetary motion. Its clarity, organization, and attempts at physical explanation made it a crucial text in disseminating and eventually accepting the Copernican worldview, despite facing religious opposition.

 

Johannes Kepler: Somnium (The dream)

Here’s an image related to Johannes Kepler’s Somnium (The Dream):

Yes, “Somnium seu Opus Posthumum de Astronomia Lunari” (The Dream, or Posthumous Work on Lunar Astronomy) is a fascinating and important work by Johannes Kepler. It’s often considered one of the earliest works of science fiction.  

Here’s what’s significant about Somnium:

• Science Fiction Narrative: Written primarily between 1608 and 1630, though not published until after Kepler’s death in 1634 by his son Ludwig, Somnium tells the story of a young Icelandic man, Duracotus, who travels to the Moon. The journey is facilitated by his sorceress mother and a demon.  
• Scientific Thought Experiment: While presented as a dream and a journey, Somnium is deeply rooted in Kepler’s scientific ideas and serves as a thought experiment exploring what the universe might look like from another celestial body, specifically the Moon.
• Lunar Astronomy: Kepler used the narrative as a vehicle to present his understanding of lunar astronomy. He discusses:
  • Lunar Geography: He describes the Moon’s surface features, speculating on mountains, valleys, and other formations based on telescopic observations of his time.
  • Lunar Motion: He incorporates his knowledge of celestial mechanics to describe the Moon’s orbit and its relationship to the Earth and the Sun.
  • Earth from the Moon: He vividly imagines how the Earth would appear from the Moon, including its phases and its apparent size and movement across the lunar sky.  
  • Habitability of the Moon: He speculates on the potential for life on the Moon, considering the extreme temperature variations between the day and night sides and imagining creatures adapted to such conditions.
• Scientific Reasoning within a Fictional Framework: Kepler cleverly weaves scientific reasoning and astronomical principles into the fictional narrative. For example, he uses the different appearances of the Earth from the Moon to explain lunar phases as seen from Earth.
• Early Example of World-Building: Somnium showcases early elements of science fiction world-building, as Kepler meticulously details the environment, inhabitants (Subvolvani and Privolvani), and conditions of the Moon based on the scientific knowledge of his era.
• Influence: Somnium is considered a significant work in the history of science fiction because it blends a fictional journey with serious scientific inquiry. It influenced later writers and thinkers who explored the possibilities of space travel and extraterrestrial life.
• Posthumous Publication: The fact that Somnium was published after Kepler’s death suggests that, given the prevailing scientific and religious views of the time, he may have viewed it as a more speculative or perhaps even controversial work during his lifetime.

In conclusion, Johannes Kepler’s Somnium is a unique and important work that bridges the gap between scientific treatise and imaginative fiction. Through a dreamlike journey to the Moon, Kepler explored lunar astronomy, the appearance of Earth from another celestial body, and the potential for extraterrestrial life, making it a fascinating early example of science fiction grounded in the scientific knowledge of the 17th century.

 

Optics

Johannes Kepler: Explanation of Vision

Here’s an image related to Johannes Kepler’s explanation of vision:

Yes, Johannes Kepler made significant and groundbreaking contributions to our understanding of how human vision works, particularly in his seminal work “Ad Vitellionem Paralipomena, Quibus Astronomiae Pars Optica Traditur” (Supplements to Vitello, in Which the Optical Part of Astronomy is Treated), published in 1604. This work is considered a cornerstone of modern optics and physiological optics.  

Here are the key aspects of Kepler’s explanation of vision:

• The Eye as an Optical Instrument: Kepler was the first to correctly describe the eye as a refracting optical instrument that forms a real, inverted image on the retina. He moved away from the ancient Greek idea that vision involved rays emanating from the eye.  
• Role of the Lens: He accurately identified the lens as the primary structure within the eye responsible for focusing light. He understood that the lens refracts (bends) the incoming light rays to converge and form a focused image.
• Image Formation on the Retina: Kepler correctly stated that the retina at the back of the eye is the surface on which the focused image is projected. He recognized that this image is real and inverted. This was a crucial departure from previous theories, which often involved the image being formed elsewhere or being upright.
• Analogy to the Camera Obscura (Pinhole Camera): As we discussed previously, Kepler used the camera obscura as an analogy to explain how the eye forms an image. He understood that just as a small hole projects an inverted image, the eye’s lens performs a similar function, focusing light through the pupil onto the retina.
• The Brain’s Role in Correcting the Image: Although he correctly described the formation of an inverted image on the retina, Kepler also realized that we perceive the world as upright. He theorized that the brain must somehow “correct” or interpret this inverted image to produce our upright perception. While he didn’t understand the neural mechanisms involved, his recognition of the brain’s active role in vision was significant.
• Accommodation (Focusing): While Kepler didn’t fully explain the mechanism of accommodation (how the eye changes focus for different distances), his understanding of the lens’s role in focusing laid the groundwork for later investigations into this process.  
• Explanation of Visual Defects: Kepler’s optical model of the eye also allowed him to begin to understand some visual defects. For example, he could conceptually link issues with the eye’s shape or the lens’s focusing power to problems like nearsightedness or farsightedness.  

Significance of Kepler’s Work:

Kepler’s explanation of vision was a revolutionary breakthrough. By applying the principles of optics to the anatomy of the eye, he established the foundation for our modern understanding of how we see. His work in “Ad Vitellionem Paralipomena” shifted from philosophical speculation to a more scientific and physical explanation of vision. His insights into the role of the lens, the formation of a real and inverted image on the retina, and the brain’s involvement were fundamental. They paved the way for future research in physiology and neuroscience.

 

Johannes Kepler: Principles of the pinhole camera

Yes, Johannes Kepler understood and described the fundamental principles of the pinhole camera (or camera obscura, as it was then known for larger versions) in his writings, particularly in the context of explaining vision and astronomical observations.  

Here’s how Kepler demonstrated his understanding:

• Analogy to the Eye: Kepler used the pinhole camera as an analogy to explain how the human eye works. He recognized that just as light passing through a small hole creates an inverted image on a surface, the lens of the eye focuses light to form an inverted image on the retina. This was a crucial step in understanding the optics of vision.  
• Formation of Inverted Images: Kepler clearly described how light rays from a scene pass through a small aperture (the pinhole) and project an inverted, real image onto a surface placed behind the pinhole. He understood that each point in the scene emits light rays traveling in all directions, but only a very narrow bundle of rays from each point passes through the small hole. These narrow bundles then strike a corresponding point on the image surface, creating a focused (though often dim) representation of the scene. The inversion occurs because rays from the top of the object pass through the pinhole and fall on the lower part of the image, and vice versa.  
• Application to Solar Observations: Kepler famously used a pinhole camera setup to safely observe the solar eclipse of 1600. He set up a dark tent with a small hole in one side. Light from the sun passed through the pinhole and projected an image of the partially eclipsed sun onto a piece of paper inside the tent. This allowed him and others to study the eclipse without directly looking at the sun, which could cause severe eye damage. His detailed observations and drawings from this event further demonstrated his practical understanding of pinhole optics.
• Explanation of Astronomical Phenomena: Kepler also used the principles of the pinhole camera to explain how light from distant objects, like the sun and moon, forms images. He understood that the small aperture effectively selects a single ray (or a very narrow beam) of light from each point on the distant object, creating a focused image.  

Key Aspects of Kepler’s Understanding:

• Inverted Image: He correctly understood that the image formed by a pinhole is inverted.
• Real Image: He knew the image was real, meaning it could be projected onto a surface.
• Light Rays: He understood that the image formation was due to light rays traveling in straight lines through the small aperture.
• Focus and Aperture Size: While he didn’t fully explore the relationship between pinhole size and image sharpness (smaller pinholes produce sharper but dimmer images), his use of the pinhole for focused solar projection indicated an understanding of the basic principle.

In conclusion, Johannes Kepler clearly understood and applied the principles of the pinhole camera in his explanations of vision and for safe astronomical observations. His use of the camera obscura as an analogy for the eye and his practical application of it for solar eclipse viewing demonstrate his grasp of this fundamental optical phenomenon.

 

Johannes Kepler: Law of Refraction (Approximate)

Here’s an image related to Johannes Kepler’s Law of Refraction (Approximate):

Yes, Johannes Kepler did work on the law of refraction, and while he didn’t derive the exact modern form we know as Snell’s Law, he did formulate an approximate law of refraction that was a significant step forward from earlier, less accurate attempts.  

Here’s what’s important about Kepler’s work on refraction:

• Context in Dioptrice (1611): Kepler’s work on refraction is primarily found in his book Dioptrice (1611), which was a comprehensive treatise on optics. In this work, he aimed to understand how lenses form images, particularly in the context of vision and telescopes.  
• Focus on the Eye and Lenses: Kepler was deeply interested in the optics of the eye and how lenses could be used to correct vision and magnify distant objects. Understanding refraction – the bending of light as it passes from one medium to another – was crucial for this.  
• Kepler’s Approximate Law: Kepler attempted to find a mathematical relationship between the angle of incidence (the angle at which light strikes a surface) and the angle of refraction (the angle at which light bends as it enters the new medium). His proposed law was an approximation, and it wasn’t universally accurate, especially for larger angles of incidence.  
• Relationship to Angles: Kepler’s approximate law often involved a direct proportionality or a linear relationship between the angles of incidence and refraction, or their complements (angles with respect to the surface). However, the actual relationship, as described by Snell’s Law, is between the sines of these angles.

Example of Kepler’s Approach: One form of Kepler’s approximate law suggested a relationship like:

(angle of incidence) / (angle of refraction) ≈ constant

•  or a similar linear relationship. While this holds reasonably well for small angles of incidence, it deviates significantly at larger angles.
• Significance as a Step Forward: Despite its approximate nature, Kepler’s work on refraction was a crucial advancement. He moved beyond qualitative descriptions and attempted to provide a mathematical framework for understanding this phenomenon. His efforts helped to focus the attention of other scientists on finding a more precise and universal law.  
• Snell’s Law (Willebrord Snellius): The exact law of refraction, now known as Snell’s Law, was formulated by the Dutch astronomer and mathematician Willebrord Snellius (though his work was not published during his lifetime). Snell’s Law states:  

n₁ sin(θ₁) = n₂ sin(θ₂)

•  Where:
  • n₁ is the refractive index of the first medium.
  • θ₁ is the angle of incidence.
  • n₂ is the refractive index of the second medium.  
  • θ₂ is the angle of refraction.
• Kepler’s Lack of Refractive Index: Kepler’s work predated the clear concept and quantification of the refractive index as a property of a medium that determines how much light bends. This concept, which is central to Snell’s Law, was developed later.

In conclusion, Johannes Kepler made a valuable early attempt to mathematically describe the law of refraction in his Dioptrice. While his formulation was an approximation and not the exact Snell’s Law, it represented a significant step towards a quantitative understanding of how light bends when passing between different media. His work helped pave the way for the later discovery of the precise law of refraction by Snellius.

 

Johannes Kepler: Keplerian telescope design

Here’s an image related to Johannes Kepler’s Keplerian telescope design:

Yes, Johannes Kepler is indeed credited with the design of the Keplerian telescope. This type of refracting telescope uses a converging (convex) lens for both the objective and the eyepiece. This design offered significant advantages over earlier refracting telescopes.

Here are the key features and benefits of the Keplerian telescope design:

• Converging Objective Lens: Like earlier refracting telescopes (often called Galilean telescopes in retrospect, even if Galileo didn’t invent the first one), the Keplerian telescope uses a large converging lens as the objective to gather light from a distant object and form a real, inverted image at its focal point.
• Converging Eyepiece Lens: The crucial difference in the Keplerian design is the use of a converging (convex) lens as the eyepiece. This eyepiece acts as a magnifying glass to view the real, inverted image formed by the objective lens.  
• Real and Inverted Image: The combination of two converging lenses produces a real and inverted final image as seen by the observer. While the image is upside down, this was not a major drawback for astronomical observations, and the benefits outweighed this inconvenience.  
• Advantages over Earlier Designs (e.g., likely what Galileo used):
  • Higher Magnification: The Keplerian design could achieve significantly higher magnifications compared to telescopes using a diverging eyepiece (which produced a virtual, upright image). The magnification is determined by the ratio of the objective lens’s focal length to the eyepiece’s focal length (Magnification ≈ f_objective / f_eyepiece). Converging eyepieces allowed for shorter focal lengths, leading to higher magnification.  
  • Wider Field of View: Keplerian telescopes generally offered a wider field of view compared to earlier refractors of similar magnification.
  • Use of Crosshairs/Micrometers: The real image formed at the focal plane between the objective and eyepiece in a Keplerian telescope allowed for the easy placement of crosshairs or micrometers for precise measurements of angular distances and positions of celestial objects. This was a significant advantage for scientific observations.
• Kepler’s Description in Dioptrice (1611): Kepler described the principles of this telescope design in his book Dioptrice (1611). While it’s not entirely clear if Kepler himself built a working telescope of this design immediately, his theoretical description laid the foundation for its subsequent development and widespread adoption by other astronomers.
• Spread and Impact: Following Kepler’s work, the Keplerian telescope design became the standard for astronomical refracting telescopes due to its superior magnification and the ability to use measuring instruments at the real image plane. Astronomers like Johannes Hevelius and Christiaan Huygens built and used long focal length Keplerian telescopes to make significant discoveries.  

In summary, the Keplerian telescope, with its use of two converging lenses for the objective and eyepiece, was a significant advancement in telescope design. It provided higher magnification, a wider field of view, and the crucial ability to use measuring instruments at the real image, making it the dominant form of refracting telescope for astronomical observations for many years. Johannes Kepler’s theoretical description in his Dioptrice was instrumental in its development and adoption.

 

Johannes Kepler: Depth Perception (Binocular Vision)

Here’s an image related to Johannes Kepler’s work on depth perception (binocular vision):

Yes, Johannes Kepler made significant early contributions to our understanding of depth perception and the role of binocular vision in this process.  

Here’s a breakdown of Kepler’s insights:

• Geometric Explanation of Binocular Vision: In his book “Dioptrice” (Dioptrics), published in 1611, Kepler provided a geometric explanation for how the two eyes work together to create a single image in the brain and how this binocular vision enables the perception of depth.  
• Disparate Images on the Retina: Kepler understood that each eye receives a slightly different image of a three-dimensional object because the eyes are positioned a certain distance apart. This difference in the images projected onto the two retinas is known as binocular disparity or stereoscopic disparity.
• Brain’s Role in Combining Images: He theorized that the brain somehow combines these two slightly different two-dimensional images into a single three-dimensional percept, giving us the sensation of depth and distance. He didn’t have the neurological understanding of how this combination occurs, but his conceptualization of the process was remarkably insightful for his time.
• Geometric Basis for Distance Judgment: Kepler recognized that the degree of disparity between the two retinal images is related to the distance of the object from the observer. Objects closer to the viewer produce a larger disparity, while objects farther away produce a smaller disparity. He essentially laid the groundwork for the idea that the brain uses this geometric difference to judge distances.  
• Focus on the Eye as an Optical Instrument: Kepler’s work in “Dioptrice” primarily focused on the eye as an optical instrument, explaining how the cornea and the lens refract light to form an image on the retina. His discussion of binocular vision was a natural extension of this optical analysis.  

Significance of Kepler’s Contribution:

Kepler’s geometric explanation of binocular vision was a crucial step in understanding depth perception. While the precise neural mechanisms of how the brain processes binocular disparity were discovered much later, Kepler’s foundational ideas about the role of the two different retinal images and their combination in the brain were highly influential. He moved beyond purely philosophical or intuitive explanations towards a more physical and geometric understanding of how we perceive the three-dimensional world.

In summary, Johannes Kepler’s work in his 1611 book “Dioptrice” provided a significant early geometric explanation of how binocular vision contributes to depth perception by recognizing the disparate images formed on the two retinas and theorizing about their combination in the brain to create a sense of depth and distance.

 

Mathematics

 

Johannes Kepler: Work of algorithms

While Johannes Kepler is not primarily known for his work on algorithms in the modern computer science sense, his work did involve systematic procedures and methods for calculation and problem-solving, which could be considered algorithmic in a broader historical context.

Here’s how we can understand Kepler’s work in relation to algorithms:

• Systematic Calculation in Astronomy: Kepler’s laws of planetary motion and his efforts to derive them from astronomical observations involved extensive and systematic calculations. For example, determining the elliptical orbits of planets and the mathematical relationships governing their speeds required meticulous data analysis and the application of specific mathematical procedures. These step-by-step methods to arrive at his laws could be seen as early forms of algorithms applied to scientific problems.  
• Geometric Constructions and Procedures: His work in geometry, particularly in Harmonices Mundi and his studies of polyhedra, involved defined sequences of steps for constructing and analyzing geometric figures. While not algorithms in the sense of computer code, these methodical approaches to geometric problems share the characteristic of a well-defined procedure.
• Methods for Determining Areas and Volumes: As discussed previously, Kepler’s “method of indivisibles” for calculating areas and volumes, while not a formal calculus, involved systematic ways of breaking down shapes into smaller parts and summing their contributions. These step-by-step approaches to solving geometric measurement problems can be considered algorithmic in nature.
• Tabulation and Organization of Data: Kepler was meticulous in his collection and organization of astronomical data. His systematic recording and arrangement of observations were crucial for his analysis and the derivation of his laws. This systematic handling of data can be seen as a precursor to algorithmic data processing.  

Distinction from Modern Algorithms:

It’s important to distinguish Kepler’s methods from modern algorithms as used in computer science:

• No Formal Programming Language: Kepler did not work within the framework of formal programming languages or automated computation. His “algorithms” were manual procedures carried out through mathematical calculations and geometric constructions.
• Focus on Mathematical and Physical Problems: His systematic methods were primarily aimed at solving problems in mathematics and physics, particularly astronomy, rather than the broader range of computational tasks that modern algorithms address.
• Level of Abstraction: Modern algorithms often involve a higher level of abstraction and generality, designed to be implemented by machines. Kepler’s methods were more directly tied to specific mathematical and physical concepts.

In conclusion, while Johannes Kepler did not work with algorithms in the way a computer scientist does today, his scientific and mathematical endeavors involved systematic and well-defined procedures for calculation, geometric construction, and data analysis. These methodical approaches to problem-solving in astronomy and mathematics can be viewed as early examples of algorithmic thinking in a historical context, even if they lacked the formal structure and automation of modern algorithms. His dedication to systematic inquiry and calculation was crucial to his groundbreaking scientific achievements.

 

Johannes Kepler: Infinitesimal Methods 

Johannes Kepler, while not considered one of the primary inventors of infinitesimal methods in the same way as Isaac Newton or Gottfried Wilhelm Leibniz, did employ ideas and techniques that can be seen as precursors to infinitesimal calculus in his work, particularly in his calculations related to areas, volumes, and the motion of celestial bodies.  

Here’s how Kepler’s work relates to infinitesimal methods:

• Method of Indivisibles: Kepler made use of a concept similar to the method of indivisibles, which was later more formally developed by Bonaventura Cavalieri. In his calculations of areas and volumes, particularly in Nova stereometria doliorum vinariorum (New Solid Geometry of Wine Barrels, 1615), Kepler treated shapes as being composed of an infinite number of infinitely small parts or “indivisibles.”
  • For example, to find the volume of a wine barrel, he conceptually slices it into a large number of thin disks or considers it generated by rotating an area composed of many small line segments. He then summed the contributions of these indivisible parts to approximate the total volume.
• Integration-like Processes: Kepler’s methods for finding areas and volumes involved processes that resemble integration, even though he lacked the formal notation and limit concepts of calculus. He essentially performed sums of very small quantities to approximate continuous totals.
• Application to Planetary Motion: In his work on planetary motion, particularly in deriving his laws, Kepler dealt with continuously changing quantities like the position and velocity of planets in their orbits. While his primary tools were geometry and algebra, his conceptualization of motion along curved paths implicitly involved considering changes over infinitesimally small intervals of time and distance.  
• Focus on Practical Problems: Kepler’s use of these early infinitesimal ideas was often driven by practical problems, such as accurately determining the volumes of wine barrels for taxation purposes or understanding the physical laws governing celestial mechanics.

Limitations Compared to Formal Calculus:

It’s crucial to understand the limitations of Kepler’s methods compared to the formal calculus developed later:

• Lack of Limits: Kepler did not have a formal concept of a limit, which is fundamental to calculus for rigorously defining derivatives and integrals. His “indivisibles” were more intuitive than precisely defined infinitesimal quantities.
• Absence of Derivatives: He did not develop the concept of a derivative as a rate of change or the slope of a tangent line.
• No Formal Algorithms: His methods were often ad hoc and specific to the problem at hand, rather than being part of a general, systematic calculus.
• Geometrical Foundation: Kepler’s approach remained largely rooted in geometry, whereas calculus provided a more algebraic and analytical framework.

Influence:

Despite these limitations, Kepler’s work with indivisible-like concepts and his attempts to quantify continuous change influenced later mathematicians who would go on to develop calculus. His intuitive approaches to dealing with the infinitely small paved the way for more formal treatments.  

In conclusion, while Johannes Kepler did not invent or fully develop infinitesimal calculus, his methods for calculating areas, volumes, and analyzing motion involved ideas that were precursors to the concepts of infinitesimals and integration. His work, driven by his investigations in astronomy and practical problems, demonstrated the power of thinking about continuous quantities in terms of infinitely small parts and contributed to the intellectual climate that eventually led to the formal development of calculus by Newton and Leibniz.

 

Johannes Kepler: Geometry of Solids/Sphere Packing

Here’s an image related to Johannes Kepler’s work on the geometry of solids/sphere packing:

Johannes Kepler made significant contributions to various areas of mathematics and physics, and his work touched upon the geometry of solids and the problem of sphere packing, although he didn’t fully solve the latter in the way we understand it today.

Here’s a breakdown of Kepler’s involvement with these topics:

Geometry of Solids:

• Harmonices Mundi (The Harmony of the Worlds, 1619): This seminal work by Kepler explored the mathematical and musical harmony he believed underlay the structure of the cosmos. In it, he extensively discussed Platonic solids (tetrahedron, cube, octahedron, dodecahedron, icosahedron) and their relationships to the orbits of the planets as he understood them through his laws of planetary motion.  
• Kepler attempted to find a geometrical basis for the spacing of the planetary orbits by nesting the Platonic solids within hypothetical spheres. While this model ultimately didn’t perfectly match the observed orbits, it demonstrated his deep interest in the geometric properties of regular solids and their potential role in the universe.
• He explored the ratios and symmetries inherent in these solids and connected them to musical intervals, seeking a unified “harmony” in God’s creation.

Sphere Packing (Kepler Conjecture):

• The Six-Cornered Snowflake (De nive sexangula, 1611): In this charming little book, Kepler pondered the question of why snowflakes always have a hexagonal shape. While doing so, he also considered the most efficient way to pack spheres.  
• Kepler observed the hexagonal close packing of spheres, which we see in things like stacked cannonballs or fruit displays. He conjectured that this hexagonal close packing (or face-centered cubic packing, which achieves the same density) represents the densest possible way to arrange identical spheres in three-dimensional space.  
• This assertion became known as the Kepler Conjecture.  
• While Kepler proposed the conjecture based on intuition and observation of natural phenomena, he did not provide a rigorous mathematical proof of its optimality. Proving that no other arrangement could achieve a higher packing density turned out to be a very difficult problem.  

The Solution to the Kepler Conjecture:

• The Kepler Conjecture remained unproven for nearly 400 years.
• In 1998, mathematician Thomas Callister Hales announced a proof of the Kepler Conjecture. Hales’ proof was extraordinarily complex and involved extensive computer calculations.  
• After a lengthy and rigorous verification process, the mathematical community finally accepted the proof.  

In summary, Johannes Kepler significantly contributed to studying the geometry of regular solids, particularly the Platonic solids, and explored their potential connection to the cosmos in his Harmonices Mundi. He also formulated the famous Kepler Conjecture regarding the densest packing of spheres based on his observations of natural phenomena like snowflakes and sphere arrangements. However, he did not provide a formal mathematical proof of this conjecture, which was finally achieved by Thomas Hales centuries later. Kepler’s intuition about sphere packing highlights his deep engagement with geometric principles in earthly and celestial realms.

 

Christiaan Huygens (1629–1695)

Huygens by Caspar Netscher (1671), Museum Boerhaave, Leiden

(Wiki Image By Caspar Netscher – http://ressources2.techno.free.fr/informatique/sites/inventions/inventions.html, Public Domain, https://commons.wikimedia.org/w/index.php?curid=44047) 

Christiaan Huygens Quotes

Christiaan Huygens (1629-1695) was a brilliant Dutch physicist, mathematician, astronomer, and inventor. While there isn’t a vast collection of widely quoted sayings attributed directly to him in the same way as some other historical figures, his writings, particularly on science and mathematics, contain insightful observations. Here are some paraphrased ideas and direct quotes that capture his thinking:

On Science and Discovery:

• Focus on Explanation: Huygens was deeply concerned with providing mechanical explanations for natural phenomena. He believed in understanding the “how” rather than just the “what.”
  • Paraphrased Idea: The true aim of science is to understand the underlying mechanisms of nature through clear and demonstrable principles.
• Importance of Observation and Experiment: While a proponent of mechanical philosophy, Huygens recognized the crucial role of empirical evidence in validating theories.
  • Paraphrased Idea: Our understanding of the world must be grounded in careful observation and experimentation.
• Mathematical Precision: Huygens was a skilled mathematician and believed that mathematical rigor was essential for scientific progress. His work on probability, optics, and mechanics reflects this.
  • Paraphrased Idea: Mathematics provides the precise language necessary to describe and analyze the laws of nature.
• The Nature of Light: His development of the wave theory of light was a groundbreaking achievement.
  • “It cannot be doubted that light consists in the motion of some sort of matter.” (This reflects his mechanical view, though his wave theory didn’t rely on a physical medium in the way he initially conceived.)
  • Paraphrased Idea: Light is not simply a point-to-point transmission but rather a propagation of a disturbance through a medium (though his understanding of this medium evolved).

On Time and the Pendulum Clock:

• His invention of the pendulum clock revolutionized timekeeping.
  • Paraphrased Idea: The regular swing of a pendulum, governed by predictable physical laws, offers a precise and reliable measure of time.
  • While not a direct quote expressing this sentiment, his dedication to perfecting the pendulum clock speaks volumes about his belief in the possibility of accurate time measurement.

On the Universe and Extraterrestrial Life (from Cosmotheoros):

Huygens was one of the first major scientists to seriously consider the possibility of extraterrestrial life in his posthumously published work, Cosmotheoros. These are paraphrased ideas from that work:

• Abundance of Planets: He reasoned that if Earth had life, then the other planets, sharing similar physical properties, likely did as well.
  • Paraphrased Idea: Given the vastness of the universe and the similarity of other planets to our own, it is highly probable that life exists elsewhere.
• Suitability of Other Worlds for Life: He speculated on the conditions on other planets and argued that they were likely suitable for some form of life, even if different from Earth’s.
  • Paraphrased Idea: Our universe’s physical laws are universal, suggesting that other celestial bodies could support life adapted to their specific environments.
• Purpose of Creation: Huygens, influenced by the prevailing theological views, often linked the existence of other worlds and life to the grandeur and purposefulness of God’s creation.
  • Paraphrased Idea: It would be inconsistent with the wisdom and power of the Creator to have made so many vast bodies serving no purpose, implying the existence of inhabitants on them.

General Reflections:

• Dedication to Study: Huygens was known for his intense focus and dedication to his scientific pursuits.
  • Paraphrased Idea: Diligent and persistent inquiry is essential for unlocking the secrets of nature.

It’s important to note that many of Huygens’s significant contributions are best understood through his scientific works and the principles he articulated within them, rather than through concise, easily quotable statements. His legacy lies in his groundbreaking theories and inventions that profoundly influenced the development of physics, astronomy, and timekeeping.

 

Christiaan Huygens YouTube Video

Christiaan Huygens

Christiaan Huygens: The Father of Modern Science | Hugh …

THE HISTORY OF THE PENDULUM CLOCK – Christiaan …

 

Christiaan Huygens History

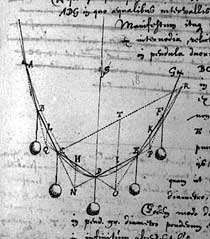
Picture of a hanging chain (catenary) in a manuscript of Huygens

(Wiki Image By Artwork by C. Huygens L. Fransen (livinus) – Unknown source, Public Domain, https://commons.wikimedia.org/w/index.php?curid=902908) 

Christiaan Huygens (April 14, 1629 – July 8, 1695) was a prominent Dutch mathematician, physicist, astronomer, and inventor, widely regarded as one of the leading scientific figures of the 17th century and a key player in the Scientific Revolution. His work spanned a remarkable range of fields, making foundational contributions to optics, mechanics, horology (timekeeping), astronomy, and mathematics.  

Here’s an overview of his history:

1. Early Life and Education (1629-1650):
   • Christiaan was born in The Hague, Dutch Republic, into an influential family. His father, Constantijn Huygens, was a renowned diplomat, poet, and composer, which provided Christiaan with an intellectually stimulating environment.  
   • He displayed early talent in mathematics and mechanics.  
   • Huygens studied law and mathematics at Leiden University (1645-1647) and then at the College of Orange in Breda (1647-1649). He benefited from correspondence and interactions with prominent intellectuals of the time, including René Descartes, a family acquaintance.  
2. Major Scientific Contributions:
   • Mechanics and Horology (Timekeeping):  
     • Pendulum Clock (c. 1656-1657): Huygens invented the first practical pendulum clock. Applying Galileo’s insights about the isochronism of pendulums (for small swings), he designed a clock mechanism that dramatically improved timekeeping accuracy, reducing errors from minutes to seconds per day. He patented this invention in 1657.  
     • Horologium Oscillatorium (The Pendulum Clock, 1673) is considered his masterpiece in mechanics. It provides a detailed mathematical analysis of pendulum motion, introduces the concept of the cycloidal pendulum (to achieve true isochronism regardless of swing amplitude), discusses the center of oscillation, and, importantly, includes the first correct mathematical formulation of centrifugal force in uniform circular motion.  
     • Laws of Collision: He also contributed fundamentally to understanding elastic collisions, deriving largely correct laws.  
   • Astronomy and Telescope Improvements:
     • Working with his brother Constantijn Huygens Jr., Christiaan became highly skilled in grinding lenses and building powerful telescopes.  
     • Discovery of Titan (1655): Huygens discovered Saturn’s largest moon, Titan, using one of their improved telescopes.  
     • True Nature of Saturn’s Rings (1656-1659): He was the first to correctly identify and describe the nature of Saturn’s mysterious appendages (which had puzzled Galileo) as a “thin, flat ring, nowhere touching [the planet], and inclined to the ecliptic.” He published this in his work Systema Saturnium (1659).  
     • Orion Nebula: He observed and sketched the Orion Nebula, resolving some of its stellar components.  
     • Huygenian Eyepiece: He developed an improved telescope eyepiece design (two plano-convex lenses) that reduced chromatic aberration, which is still known by his name.  
   • Optics (Wave Theory of Light):
     • Huygens is famous for proposing a wave theory of light, in contrast to Newton’s corpuscular theory.  
     • Traité de la Lumière (Treatise on Light, published 1690, written c. 1678): In this seminal work, he articulated Huygens’ Principle, which states that every point on a wavefront can be considered as a source of secondary spherical wavelets. Using this principle, he provided elegant explanations for the laws of reflection and refraction of light, and also described the phenomenon of birefringence (double refraction) in Iceland spar.  
   • Mathematics:
     • He wrote one of the earliest printed treatises on probability theory, De Ratiociniis in Ludo Aleae (On Reasoning in Games of Chance), published in 1657 as an appendix to a work by Frans van Schooten. This was based on earlier correspondence between Pascal and Fermat.  
     • He also worked on various curve-related problems, such as the catenary and the tractrix.  
3. Career, Affiliations, and Later Life (c. 1650-1695):
   • Huygens gained an international reputation early in his career.  
   • He made several visits to England and became a Fellow of the Royal Society of London in 1663.  
   • From 1666 to 1681, he lived and worked in Paris under the patronage of King Louis XIV, becoming a founding and leading member of the French Royal Academy of Sciences (Académie Royale des Sciences). This was a period of great productivity.
   • Due to ill health and the increasingly anti-Protestant climate in France (culminating in the Revocation of the Edict of Nantes in 1685), he returned to The Hague in 1681, where he continued his scientific work.  
   • In his later years, he wrote Cosmotheoros (published posthumously in 1698), speculating on the existence of extraterrestrial life and planetary conditions.  
4. Death and Legacy:
   • Christiaan Huygens died in The Hague on July 8, 1695.  
   • He stands as one of the most influential scientists of the 17th century, bridging the work of Galileo and Newton. His contributions to physics (especially mechanics and optics), astronomy, mathematics, and engineering (horology) were profound and lasting. Though largely overshadowed by Newton’s particle theory for over a century, his wave theory of light was eventually revived and became a cornerstone of modern optics. The Cassini-Huygens space probe mission to Saturn and Titan was named in honor of him and Giovanni Cassini.

 

Christiaan Huygens Discoveries Table

Okay, here is a table summarizing Christiaan Huygens’s major scientific discoveries and contributions across various fields:

Discovery/Contribution	Significance/Details/Associated Work
Astronomy
True Nature of Saturn’s Rings	(1656-1659) Correctly proposed that Saturn is surrounded by a thin, flat, detached ring system, explaining its changing appearance. Published in Systema Saturnium (1659).
Discovery of Titan	(1655) Discovered Saturn’s largest moon, Titan, using a telescope he and his brother built.
Observations of the Orion Nebula	Resolved parts of the Orion Nebula into individual stars and provided early, detailed sketches.
Telescope Improvements	Developed superior lens grinding techniques and designed the Huygenian eyepiece, which reduced chromatic aberration and offered a wider field of view.
Physics: Mechanics & Horology
Invention of the Pendulum Clock	(c. 1656-1657) Invented the first practical pendulum clock, dramatically increasing timekeeping accuracy from minutes to seconds per day. Patented in 1657.
Theory of Pendulums	Horologium Oscillatorium (1673) provided a comprehensive mathematical analysis of pendulum motion, including the concept of the cycloidal pendulum, which achieves isochronism even with larger swings.
Laws of Elastic Collision	Formulated largely correct laws governing the collision of elastic bodies, improving upon Descartes’ earlier work. (Work was largely done by the 1650s, and it was published later.)
Centrifugal Force	Provided the first correct quantitative formula for centrifugal force (Fc​=mv2/r). Detailed in Horologium Oscillatorium and his posthumous De Vi Centrifuga.
Physics: Optics
Wave Theory of Light	Proposed that light propagates as a wave, in contrast to Newton’s corpuscular theory. Developed in the 1670s, published in Traité de la Lumière (Treatise on Light, 1690).
Huygens’ Principle	Stated that every point on a wavefront can be considered a source of secondary spherical wavelets, the envelope of which forms the new wavefront. Used to explain reflection and refraction.
Explanation of Birefringence	He provided a wave-based explanation for the phenomenon of double refraction in Iceland spar (calcite), which was a key success of his wave theory.
Mathematics
Probability Theory	Wrote De Ratiociniis in Ludo Aleae (On Reasoning in Games of Chance, 1657), one of the earliest printed works on probability, introducing concepts like expected value.
Work on Curves	Studied various mathematical curves, including the catenary (shape of a hanging chain), tractrix, and the properties of evolutes and involutes (related to his pendulum work).

Export to Sheets

Christiaan Huygens was a leading figure in the Scientific Revolution, making foundational contributions that significantly advanced multiple scientific disciplines.

 

Astronomy

Christiaan Huygens: True nature of Saturn’s rings

Here’s an image related to Christiaan Huygens’ discovery of the true nature of Saturn’s rings:

Christiaan Huygens, the brilliant 17th-century Dutch scientist, was the first to correctly determine the true nature of Saturn’s rings, solving a puzzle that had perplexed astronomers since Galileo first observed Saturn’s strange, changing appearance.  

Here’s a summary of his discovery:

1. The Preceding Mystery:
   • When Galileo Galilei first observed Saturn with his telescope around 1610, its resolution wasn’t sufficient to discern rings. He initially described Saturn as a “triple-bodied” planet, or as having “handles” or “ears” on either side.  
   • Over the following decades, astronomers were baffled as these “appendages” changed shape and sometimes disappeared entirely, only to reappear later. Various hypotheses were proposed, including Saturn being an ellipsoidal planet with attached lobes or having two large moons very close to it.
2. Huygens’s Observations and Improved Telescopes:
   • Starting around 1655, Christiaan Huygens, using telescopes he and his brother Constantijn had significantly improved with superior lens-grinding techniques (achieving around 50x magnification initially for these observations), began meticulously observing Saturn.  
   • His more powerful and clearer telescopes allowed him to see details that had eluded previous observers.
3. The Hypothesis of a Ring:
   • Through careful observation and brilliant deductive reasoning, Huygens concluded that Saturn was surrounded by a “thin, flat ring, nowhere touching [the planet], and inclined to the ecliptic.”  
   • This was a revolutionary idea. He proposed that this single, solid (as he initially conceived it) ring, tilted at an angle to Saturn’s orbital plane (and thus to our line of sight from Earth), would account for all the perplexing changes in Saturn’s appearance.
4. Explanation of Appearances:
   • Huygens’s ring theory elegantly explained why Saturn sometimes appeared with “handles” (when the rings were open and wide from Earth’s perspective), why these handles would sometimes appear to shrink, and why they would periodically “disappear” entirely (when Earth passed through the plane of the rings, making them visible only as a thin line, too faint for early telescopes to resolve distinctly).  
5. Securing Priority (Anagram):
   • To secure priority for his groundbreaking explanation while he continued to refine his observations and theory, Huygens first published his solution in 1656 as an anagram in Pierre Borel’s book De vero telescopii inventore and also at the end of his own short work De Saturni Luna Observatio Nova (which announced his discovery of Titan).  
   • The decoded anagram read (in Latin): “Annulo cingitur, tenui, plano, nusquam cohaerente, ad eclipticam inclinato” (It is surrounded by a thin, flat ring, nowhere touching, and inclined to the ecliptic).  
6. Full Publication – Systema Saturnium (1659):  
   • Huygens presented his complete theory, observations, diagrams illustrating the changing aspects of the rings, and arguments against previous hypotheses in his seminal work, Systema Saturnium (The Saturnian System), published in 1659.  
   • This work provided a coherent and compelling explanation that became widely accepted.
7. Significance:
   • Huygens’s correct interpretation of Saturn’s rings was a major triumph of early telescopic astronomy and physical reasoning.  
   • It solved one of the greatest astronomical puzzles of the 17th century.
   • It further demonstrated the power of improved optical instruments and meticulous observation combined with sharp intellect.  
   • It expanded the understanding of the complexity and diversity of celestial bodies within the solar system.

While later observations by astronomers like Giovanni Cassini would reveal that the rings were not a single solid structure but composed of multiple rings and countless small particles, Huygens’s fundamental insight that Saturn was surrounded by a detached, thin, flat ring system was a monumental step forward.

 

Christiaan Huygens: Discovery of Titan

Christiaan Huygens, the brilliant 17th-century Dutch scientist, is credited with the discovery of Saturn’s largest moon, Titan. Here are the key historical details of this important astronomical finding:  

1. Date of Discovery: Huygens discovered Titan on March 25, 1655.  
2. Telescope Used: He made the discovery using a refracting telescope that he and his brother, Constantijn Huygens Jr., had designed and built themselves. They were highly skilled in grinding and polishing lenses, which allowed them to construct telescopes of superior quality and magnification (around 50x for the one used for Titan’s discovery, with a focal length of about 12 feet or 3.6 meters) compared to many available at the time.  
3. Method of Observation and Confirmation: Huygens observed a bright point of light near Saturn. He meticulously tracked its position over several nights to confirm it was a moon and not a background star. He observed its consistent motion relative to Saturn, allowing him to deduce that it was orbiting the planet and to calculate its approximate orbital period (which he determined to be about 16 days).
4. Initial Naming and Publication:
   • Huygens initially referred to his discovery simply as “Luna Saturni” (Latin for “Saturn’s Moon”).  
   • To secure his priority while continuing observations, he first announced the discovery in the form of an anagram in a short pamphlet titled De Saturni Luna Observatio Nova (A New Observation of Saturn’s Moon) published in March 1656.  
   • In his more comprehensive work on Saturn, Systema Saturnium, published in 1659, he provided a full account of the discovery, including his calculations of its orbit. This book also famously contained his correct explanation of Saturn’s rings.  
5. Significance of the Discovery:
   • Titan was the first moon of Saturn to be discovered.  
   • It was only the sixth planetary moon known at the time (after Earth’s Moon and the four Galilean moons of Jupiter discovered by Galileo in 1610).  
   • This discovery further supported the Copernican view of the solar system by demonstrating another planet with its own satellite system, implying that Earth was not the sole center of celestial motion.
   • It highlighted the advancements in telescope technology and observational astronomy.  
6. Eventual Naming: The name “Titan” (after the mythological Greek Titans, siblings of Cronus, the Greek equivalent of the Roman god Saturn) was not given by Huygens. It was proposed much later, in 1847, by John Herschel, who suggested names for the then-known seven moons of Saturn to avoid confusion with numerical designations.  

Christiaan Huygens’s discovery of Titan was a significant milestone in the exploration of our solar system and a testament to his skill as an observer and instrument maker.

 

Christiaan Huygens: Observations of Orion nebula

Here’s an image related to Christiaan Huygens’ observations of the Orion Nebula:

Christiaan Huygens, the renowned 17th-century Dutch scientist, made significant early telescopic observations of the Orion Nebula (also known as M42 or NGC 1976). Here’s what is historically noted about his work on this celestial object:  

1. Date of Observation: Huygens is credited with independently discovering or, more accurately, providing the first detailed study and sketch of the Orion Nebula around 1656. While the nebula is faintly visible to the naked eye and had been noted by a few earlier observers with telescopes (like Nicolas-Claude Fabri de Peiresc in 1610 and Johann Baptist Cysat in 1618), Huygens’s work was more thorough.  
2. Telescopic Power: He used his own significantly improved refracting telescopes, which he and his brother Constantijn had become skilled at grinding and constructing. These telescopes offered greater magnification and clarity than many of their contemporaries.  
3. Description and Sketch:
   • Huygens described the nebula not just as a cloudy patch but as a “portent in the sky” or an “opening in the sky” (a “hiatus” or “lucid spot”) through which one seemed to be looking into a more luminous region beyond.
   • He was the first to provide a detailed sketch of the central region of the nebula. His drawing identified several individual stars embedded within the nebulosity, most notably three of the four bright stars that form the asterism now known as the Trapezium Cluster at the heart of the nebula. (The fourth prominent star of the Trapezium was first clearly resolved a bit later).  
4. Publication: His observations and the sketch of the Orion Nebula were published in his landmark 1659 work, Systema Saturnium. Although this book was primarily dedicated to his discoveries about Saturn (its rings and the moon Titan), it also included other significant astronomical observations. The brightest central part of the Orion Nebula is still sometimes referred to as the “Huygenian Region” or “Huygens Region” in honor of his pioneering study.  
5. Significance:
   • Huygens’s work represented one of the first detailed telescopic studies and depictions of a deep-sky nebula.
   • His ability to resolve individual stars within the nebula was a testament to the quality of his telescopes and his observational skill.
   • It contributed to the growing body of evidence gathered by early telescopic astronomers that the heavens were far more complex and detailed than previously imagined.
   • While the true nature of nebulae as vast clouds of gas and dust, often sites of star formation, would not be understood until much later, Huygens’s observations marked an important early step in their study.

Christiaan Huygens’s observations of the Orion Nebula stand as a significant achievement in the early history of telescopic astronomy, showcasing his skill as an observer and instrument maker.

 

Christiaan Huygens: Telescope Improvements

Here’s an image related to Christiaan Huygens’ telescope improvements:

Christiaan Huygens significantly improved telescopes, particularly refracting telescopes (those that use lenses to focus light). His advancements were crucial for his astronomical discoveries, such as the true shape of Saturn’s rings and the discovery of its largest moon, Titan.  

Here are the key areas where Huygens improved telescopes:

• Lens Grinding and Design:
  • Huygens, often working with his brother Constantijn, dedicated considerable effort to grinding and polishing high-quality lenses with long focal lengths. These long focal lengths were essential for reducing chromatic aberration (the color fringing that occurs in simple lenses) and spherical aberration (blurring due to the spherical shape of the lens).  
  • By meticulously crafting lenses with smoother surfaces and more accurate curvatures, Huygens was able to build telescopes with higher magnification and clearer images compared to those available previously.
• Aerial Telescopes (Tubeless Telescopes):  
  • To overcome the limitations of building very long and stable telescope tubes (which could flex and cause misalignment), Huygens pioneered the development of aerial telescopes or tubeless telescopes.  
  • In these designs, the objective lens (the large lens at the front) was mounted on a tall pole or a building, and the eyepiece (the smaller lens you look through) was held separately by the observer, often connected by a string or a long rod to maintain alignment.
  • The long distance between the objective lens and the eyepiece (the focal length) provided high magnification without the need for an unwieldy and unstable long tube.
  • Huygens published his work on these designs in “Astroscopia Compendiaria” (Concise Account of Telescopes) in 1684, detailing the construction and advantages of aerial telescopes. While cumbersome to use, these telescopes were instrumental in achieving high magnifications before more stable long tubes could be effectively manufactured.  
• The Huygenian Eyepiece:
  • Another important invention by Huygens was the Huygenian eyepiece, developed around 1662. This eyepiece consisted of two plano-convex lenses with their convex sides facing the objective lens.
  • The Huygenian eyepiece was designed to reduce chromatic aberration and provided a wider and sharper field of view compared to single-lens eyepieces.
  • While not completely free of chromatic aberration, it offered a significant improvement and became a standard eyepiece design for many telescopes for over a century. It is still used in some applications today, particularly in simpler telescopes and microscopes.  

Impact of Huygens’ Telescope Improvements:

Huygens’ advancements in telescope technology directly enabled his significant astronomical discoveries:  

• Discovery of Titan (1655): Using a telescope with a long focal length and improved lenses that he likely ground himself, Huygens discovered Titan, the largest moon of Saturn.  
• Determination of Saturn’s Rings (1659): Through his superior telescopes, Huygens was the first to correctly identify the true shape of Saturn’s rings as a thin, flat ring encircling the planet and not touching it. He was able to observe its changing appearance from Earth due to the planet’s tilt.

In summary, Christiaan Huygens was a key figure in the improvement of telescopes during the 17th century. His dedication to crafting high-quality lenses, his innovative design of aerial telescopes, and his invention of the Huygenian eyepiece significantly enhanced the power and clarity of astronomical observations, leading directly to his own groundbreaking discoveries about Saturn and its moon Titan. His contributions laid the groundwork for further advancements in telescope technology.

 

Physics: Mechanics and horology

Christiaan Huygens: Invention of the pendulum clock

Here’s an image related to Christiaan Huygens’ invention of the pendulum clock:

Christiaan Huygens is widely credited with the invention of the pendulum clock in 1656/1657. This invention was a monumental leap forward in the accuracy of timekeeping, far surpassing the precision of earlier mechanical clocks that relied on balance wheels and folios.  

Here’s a breakdown of the key aspects of Huygens’ invention:

• Motivation: Accurate Timekeeping: Huygens was deeply interested in accurate time measurement for both scientific purposes (particularly astronomy and determining longitude at sea) and practical applications. Existing clocks were significantly inaccurate, leading to errors in navigation and scientific observations.  
• Galileo’s Observation: The principle behind the pendulum clock was based on Galileo Galilei’s earlier observation (around 1583) of the isochronism of small oscillations of a pendulum. Galileo noticed that the period of swing of a pendulum is approximately independent of the amplitude (the extent of the swing), especially for small angles.  
• Huygens’ Adaptation and Improvement: Galileo had the initial idea, but didn’t successfully build a working pendulum clock. Huygens adapted Galileo’s principle into a practical and accurate timekeeping device through his understanding of mechanics and his ingenuity.  
• Key Components of Huygens’ Pendulum Clock:
  • Pendulum as the Timekeeper: The heart of the invention was the pendulum, a weight suspended from a pivot point that swings back and forth under the influence of gravity. The regular and predictable period of the pendulum’s swing provided a consistent time interval.  
  • Escapement Mechanism: To maintain the pendulum’s oscillations against friction and air resistance, Huygens designed an escapement mechanism. This mechanism interacts with the pendulum to give it a small push on each swing, thus regulating the unwinding of the clock’s mainspring (the power source) and ensuring a steady and controlled release of energy to the pendulum. While the search snippet suggests Galileo designed an escapement, it was Huygens’ design that was successful and widely adopted in pendulum clocks. Different types of escapements were developed over time, but Huygens’ initial design was crucial.  
  • Gear Train: A series of gears (the gear train) was connected to the escapement mechanism to translate the regular oscillations of the pendulum into the movement of clock hands that displayed the time.  
  • Power Source: A wound mainspring (or sometimes a falling weight in larger clocks) provided the energy to drive the entire mechanism.
• Impact and Advantages: Huygens’ pendulum clock offered a significant improvement in accuracy, with errors of only a few seconds per day, compared to the minutes or even hours of error per day in earlier clocks. This breakthrough had a profound impact on:
  • Navigation: More accurate timekeeping allowed for more precise determination of longitude at sea, making voyages safer and more efficient.  
  • Astronomy: Precise time measurements were crucial for astronomical observations and calculations.  
  • Scientific Research: Accurate timing became essential for various scientific experiments.
  • Everyday Life: Eventually, pendulum clocks became more accessible and influenced the organization of daily life.
• Publication: Huygens detailed his invention and the underlying theory in his groundbreaking book “Horologium Oscillatorium sive de motu pendulorum” (The Pendulum Clock and the Motion of Pendulums), published in 1673. This work contained not only the description of his clock but also a rigorous mathematical analysis of pendulum motion and related mechanical principles.  

In summary, Christiaan Huygens’ invention of the pendulum clock in the mid-1650s was a pivotal moment in the history of timekeeping and science. By successfully applying Galileo’s observation of pendulum isochronism and developing the necessary mechanical components like an efficient escapement, Huygens created a far more accurate and reliable timekeeping device that had a lasting impact on navigation, astronomy, scientific research, and ultimately, society.

 

Christiaan Huygens: Theory of pendulums

Here’s an image related to Christiaan Huygens’ theory of pendulums:

Christiaan Huygens made groundbreaking contributions to the theory of pendulums, primarily documented in his monumental work “Horologium Oscillatorium sive de motu pendulorum” (The Pendulum Clock and the Motion of Pendulums), published in 1673. This work was far more than just a description of his invention of the pendulum clock; it contained a rigorous mathematical analysis of pendulum motion and related concepts in mechanics.  

Here are the key aspects of Huygens’ theory of pendulums:

• Isochronism and the Cycloid: Huygens was deeply concerned with the isochronism of pendulum oscillations, which is the property that the period of swing should be independent of the amplitude. He recognized that the period of a simple pendulum (swinging in a circular arc) is only approximately isochronous for small amplitudes. Through his mathematical analysis, he discovered that a pendulum swinging along a cycloidal arc is perfectly isochronous.
• The Cycloidal Pendulum: To achieve isochronous motion, Huygens designed a cycloidal pendulum. This involved suspending the pendulum bob with a string that would partially wrap around curved cheeks (shaped like evolutes of a cycloid) on either side of the suspension point. This contrivance forced the pendulum bob to move along a cycloidal path. While practically challenging due to friction and string flexibility, this was a significant theoretical breakthrough.  

Period of the Cycloidal Pendulum: Huygens derived the formula for the period of a cycloidal pendulum:

T = 2π√(4R/g) = 2π√(L/g)

•  Where:
  • T is the period of oscillation.
  • π is pi.
  • R is the radius of the generating circle of the cycloid.
  • g is the acceleration due to gravity.
  • L = 4R is the effective length of the cycloidal pendulum (related to the diameter of the generating circle).
• This formula shows that the period depends only on the length and the acceleration due to gravity, and not on the amplitude.
• Compound Pendulum (Physical Pendulum): Huygens also extended his analysis to the compound pendulum or physical pendulum, which is any rigid body that oscillates about a fixed axis. He determined the concept of the center of oscillation – a point in a physical pendulum where, if all its mass were concentrated, it would have the same period as the physical pendulum. This was crucial for understanding the behavior of real-world pendulums that are not idealized point masses.
• Relationship Between Length and Period: Huygens established the precise mathematical relationship between a pendulum’s length and period, both for simple and cycloidal pendulums. This was fundamental for using pendulums as accurate timekeeping devices.  
• Influence on Clockmaking: Huygens’ theoretical work directly led to his invention of the pendulum clock in 1656/1657, a revolutionary invention that significantly improved the accuracy of timekeeping compared to earlier mechanical clocks. His understanding of isochronism was central to this invention.  
• Further Investigations in Horologium Oscillatorium: His book went beyond just pendulums, delving into the motion of bodies in a vacuum along various curves, including the cycloid. He also explored concepts like centrifugal force in the context of circular motion, which was relevant to understanding the forces acting on a pendulum bob.  

In summary, Christiaan Huygens’ theory of pendulums was a landmark achievement in mechanics and horology. He not only invented the practical pendulum clock but also provided a rigorous mathematical framework for understanding pendulum motion, including the crucial concept of isochronism and the unique properties of the cycloidal pendulum. His work laid the foundation for accurate timekeeping and contributed significantly to the development of classical mechanics.

 

Christiaan Huygens: Laws of Elastic Collision

Here’s an image related to Christiaan Huygens’ Laws of Elastic Collision:

Christiaan Huygens made foundational contributions to the understanding of elastic collisions in physics during the mid-17th century, significantly correcting and advancing the prevailing theories, particularly those of René Descartes.  

Here’s an overview of his work on this topic:

1. Context – Prevailing Theories: Before Huygens, René Descartes had proposed a set of laws of impact. However, several of Descartes’s rules were incorrect because they did not adequately account for the direction of motion (i.e., velocity as a vector) and relied on a scalar concept of “quantity of motion” (mass times speed).
2. Huygens’s Approach and Key Principles: Huygens, largely through logical deduction and ingenious use of the principle of relativity of motion, arrived at a set of correct laws for perfectly elastic collisions. His key insights and rules, developed primarily in the 1650s, included:
   • Relativity of Motion: A crucial element of Huygens’s approach was realizing that the laws of physics (including collisions) must be the same in all inertial frames of reference. He often analyzed collisions by transforming to a frame of reference where the center of mass of the colliding bodies is at rest, simplifying the problem.
   • Conservation of “Quantity of Motion” (Momentum): Huygens understood that, in a closed system, the total “quantity of motion” (effectively momentum, taking direction into account) remains constant. His fifth rule explicitly states: “The quantity of motion of two bodies can increase or decrease through impact; but always there remains the same amount in the same direction, after the quantity of the motion in the opposite direction has been subtracted.”
   • Conservation of Vis Viva (related to Kinetic Energy): For perfectly elastic collisions, Huygens demonstrated the conservation of the sum of the product of each body’s mass and the square of its velocity (mv2). This quantity, later termed vis viva by Leibniz, is directly proportional to what we now call kinetic energy. His sixth rule states: “The sum of the products of the mass [moles] of each hard body multiplied by the square of its velocity is always the same before and after impact.”  
   • Relative Velocity: He formulated a rule stating that for a direct elastic collision between two bodies, their relative velocity of separation after the impact is equal in magnitude (and opposite in direction for the reversed velocities) to their relative velocity of approach before the impact.
3. Methodology: Huygens did not primarily rely on extensive experimentation for these laws (though he did conduct some) but rather on a series of logical postulates and the principle of Galilean relativity – that the outcome of an experiment should be the same whether viewed from a stationary frame or a frame moving at a constant velocity (like a boat).
4. Publication and Dissemination:
   • Huygens had largely formulated his laws of collision by 1656 in a manuscript titled De Motu Corporum ex Percussione (On the Motion of Bodies by Percussion).
   • He communicated a summary of his rules to the Royal Society of London in 1668, and they were published in the Journal des Sçavans and the Philosophical Transactions of the Royal Society in 1669.  
   • The full treatise, De Motu Corporum ex Percussione, was published posthumously in his Opuscula Posthuma in 1703.
5. Significance:
   • Huygens’s work provided the first largely correct and mathematically sound theory of elastic collisions, superseding the flawed rules of Descartes.
   • His principles laid important groundwork for Isaac Newton’s development of classical mechanics and the laws of motion, particularly the concept of momentum and the conservation principles.
   • His use of the relativity of motion was a powerful analytical tool.

Christiaan Huygens’s contributions to the understanding of elastic collisions were a major step forward in the development of classical mechanics during the Scientific Revolution.

 

Christiaan Huygens: Centrifugal Force

Here’s an image related to Christiaan Huygens’ work on Centrifugal Force:

Christiaan Huygens made a significant and correct contribution to understanding centrifugal force. In his work “De Vi Centrifuga” (On Centrifugal Force), written in 1659 but published posthumously in 1703, Huygens derived the quantitative law for centrifugal force acting on an object moving in uniform circular motion.  

Here’s a breakdown of Huygens’ contribution:

• First Mathematical Formulation: Huygens was the first to express the centrifugal force mathematically and correctly. While others before him had intuited the outward “force” associated with circular motion, Huygens provided a precise formula.  
• Dependence on Mass, Velocity, and Radius: He correctly determined that the magnitude of the centrifugal force is:
  • Directly proportional to the mass (m) of the object. A heavier object requires a greater force to keep it moving in a circle.
  • Directly proportional to the square of the velocity (v²) of the object. The faster the object moves, the greater the outward force.
  • Inversely proportional to the radius (r) of the circular path. A tighter circle (smaller radius) requires a greater force to maintain the circular motion.  

Huygens’ Formula (in modern notation): While Huygens didn’t use modern algebraic notation, his findings can be expressed as:

F_c = mv²/r

•  Where:
  • F_c represents the centrifugal force.
  • m is the mass of the object.  
  • v is the speed of the object.  
  • r is the radius of the circular path.
• Distinction from Centripetal Force: It’s important to note that Huygens focused on the centrifugal force, which is the apparent outward force experienced by an object moving in a circular path from the perspective of a rotating frame of reference (i.e., from the perspective of the object itself). The centripetal force, on the other hand, is the real inward force that is required to keep an object moving in a circle. Newton later formalized the concept of centripetal force as the cause of circular motion in his laws of motion. However, Huygens’ work on centrifugal force was crucial in understanding the dynamics of circular motion.  
• Geometric Derivation: Huygens derived his law geometrically, relying on concepts of instantaneous velocity and changes in direction in circular motion. He did this before the full development of calculus by Newton and Leibniz.  
• Influence on Newton: Huygens’ work on centrifugal force was known to Isaac Newton and is believed to have influenced Newton’s development of his laws of motion and his understanding of gravity. The concept of centrifugal force played a role in Newton’s analysis of planetary motion and the inverse-square law of gravitation.

In summary, Christiaan Huygens was the first to mathematically formulate the law of centrifugal force for uniform circular motion, correctly identifying its dependence on mass, the square of velocity, and the inverse of the radius. His work was a significant contribution to classical mechanics and played a role in the later development of Newton’s laws of motion and the theory of gravitation. While we now understand circular motion primarily in terms of the centripetal force, Huygens’ rigorous analysis of the apparent outward force was a crucial step in understanding the dynamics of objects moving in curved paths.

 

Physics: Optics

Christiaan Huygens: Wave Theory of Light

Here’s an image related to Christiaan Huygens’ Wave Theory of Light:

Christiaan Huygens’ wave theory of light, primarily outlined in his seminal work “Traité de la Lumière” (Treatise on Light) published in 1690, offered a groundbreaking alternative to the prevailing corpuscular (particle) theory championed by Isaac Newton at the time. While Newton’s theory held sway for many years, Huygens’ wave theory eventually became a cornerstone of modern optics.  

Here are the key tenets of Huygens’ wave theory of light:

• Light as a Wave: Huygens proposed that light is not a stream of particles but rather a wave that propagates through a medium he called the luminiferous ether. He envisioned this ether as a pervasive, elastic substance filling all space, even vacuums.  
• Huygens’ Principle: The core of his theory lies in Huygens’ Principle, which states that:
  • Every point on a wavefront may be regarded as a source of secondary spherical wavelets that spread out in the forward direction at the speed of the wave.  
  • The new wavefront at a later time is the envelope (the tangential surface) of all these secondary wavelets.  
• Explanation of Optical Phenomena: Using this principle, Huygens successfully provided geometrical explanations for several known properties of light:
  • Rectilinear Propagation: In a uniform medium, the secondary wavelets from a planar wavefront create a new planar wavefront that continues to move in a straight line.
  • Reflection: When a wavefront strikes a reflecting surface, the parts of the wavefront that hit the surface become sources of reflected wavelets. The envelope of these reflected wavelets forms a new wavefront that obeys the law of reflection (angle of incidence equals angle of reflection).  
  • Refraction: When a wavefront passes from one medium to another where the speed of light is different, the wavelets in the new medium travel at a different speed. This difference in speed causes the wavefront to bend at the interface, explaining Snell’s Law of refraction.
  • Double Refraction (Birefringence): Huygens also attempted to explain the peculiar phenomenon of double refraction observed in calcite crystals. He postulated that in such crystals, light propagated with two different wavefront shapes (spherical for the ordinary ray and ellipsoidal for the extraordinary ray), leading to the two refracted rays.  

Strengths of Huygens’ Wave Theory:

• Elegant Explanations: It provided coherent and geometrical explanations for reflection and refraction, including the derivation of Snell’s Law.  
• Prediction of Speed Change: It correctly predicted that light would travel more slowly in a denser medium (like water or glass) compared to a rarer medium (like air or vacuum), which was later experimentally confirmed. This was opposite to Newton’s corpuscular theory, which implied light would travel faster in a denser medium.  

Weaknesses and Limitations:

• Nature of the Ether: The luminiferous ether was a hypothetical medium that was never directly observed and posed many theoretical difficulties.  
• Longitudinal Waves: Huygens initially conceived of light waves as longitudinal (vibrations parallel to the direction of propagation), similar to sound waves. This made it difficult to explain phenomena like polarization, which requires transverse waves (vibrations perpendicular to the direction of propagation). 
• Intensity and Interference: Huygens’ original principle didn’t inherently explain the intensity of light or the phenomena of interference and diffraction in a quantitative way. While he could qualitatively describe how waves might spread (related to diffraction), a full understanding of these phenomena required the later additions by Fresnel (the Huygens-Fresnel principle).

Historical Context and Legacy:

Despite its successes, Huygens’ wave theory was not immediately accepted, largely due to the immense authority of Isaac Newton and the apparent success of his corpuscular theory in explaining rectilinear propagation. It wasn’t until the early 19th century, with the work of Thomas Young on interference and Augustin-Jean Fresnel on diffraction, that the wave theory of light gained strong experimental support and was revived and further developed, building upon Huygens’ foundational ideas.  

In conclusion, Christiaan Huygens’ wave theory of light, centered around Huygens’ Principle, was a revolutionary contribution to optics. Although it had limitations and was initially overshadowed by the corpuscular theory, it laid the essential groundwork for the modern understanding of light as a wave phenomenon and proved crucial for explaining reflection, refraction, and, eventually, with further developments, interference and diffraction.

 

Christiaan Huygens: Huygens’ Principle

Here’s an image related to Christiaan Huygens’ Principle:

Huygens’ Principle is a fundamental concept in wave optics, developed by Christiaan Huygens and presented in his Treatise on Light (1690). It provides a geometrical way to understand and predict the propagation of waves, including light waves.  

Here’s the essence of Huygens’ Principle:

Every point on a wavefront may be regarded as a source of secondary spherical wavelets that spread out in the forward direction at the speed of the wave. The new wavefront at a later time is the envelope (the tangential surface) of all these secondary wavelets.  

Let’s break down this principle:

• Wavefront: A wavefront is a surface connecting points in the same oscillation phase in a wave. For example, the crests of a series of water waves form a wavefront.  
• Secondary Wavelets: According to Huygens, each point on this initial wavefront acts as a new source, emitting its spherical wave, called a wavelet. These wavelets travel at the same speed as the original wave.  
• Envelope: The new wavefront is determined slightly later by drawing a tangent surface to all of these secondary wavelets. This new envelope represents the position and shape of the wave as it propagates.  
• Forward Direction: Huygens initially postulated that these secondary wavelets only propagate in the forward direction of the wave’s motion. He didn’t have a complete explanation for why they also didn’t travel backward. Fresnel later addressed this issue with the Huygens-Fresnel principle, which incorporates the concept of interference.  

How Huygens’ Principle Explains Wave Phenomena:

Huygens successfully used his principle to explain several key properties of light:  

• Rectilinear Propagation: In a uniform medium, the secondary wavelets from a planar wavefront will create a new one that continues moving in a straight line.
• Reflection: When a wavefront strikes a reflecting surface, the parts of the wavefront that hit the surface become sources of reflected wavelets. The envelope of these reflected wavelets forms a new wavefront that obeys the law of reflection (angle of incidence equals angle of reflection).  
• Refraction: When a wavefront passes from one medium to another where the speed of light is different, the wavelets in the new medium travel at a different speed. This difference in speed causes the wavefront to bend at the interface, explaining Snell’s Law of refraction.  
• Diffraction: While Huygens’ original principle provided a qualitative idea of how waves might spread out after passing through an aperture, a full explanation of diffraction required the later additions by Fresnel, incorporating the interference of the secondary wavelets.  

Limitations of Huygens’ Original Principle:

Despite its success, Huygens’ original principle had some limitations:  

• Backward Propagation: As mentioned, it didn’t explain why the secondary wavelets only travel forward.
• Intensity Distribution: It didn’t provide a way to calculate the amplitude or intensity of the new wavefront.

The Huygens-Fresnel Principle:

Augustin-Jean Fresnel later extended Huygens’ Principle by incorporating the concept of interference of the secondary wavelets. The Huygens-Fresnel Principle states that the amplitude of the light at a point on the new wavefront is the superposition (sum) of the amplitudes of all the secondary wavelets arriving at that point, taking into account their relative phases. This refined principle could successfully explain diffraction and other interference phenomena.  

In conclusion, Huygens’ Principle was a revolutionary idea that established the wave nature of light and provided a powerful geometric tool for understanding its propagation and behavior when it interacts with surfaces and passes through different media. While Fresnel later refined it, Huygens’ original formulation laid the foundation for the modern understanding of wave optics.

 

Christiaan Huygens: Explanation of Birefringence

Here’s an image related to Christiaan Huygens’ explanation of Birefringence:

Christiaan Huygens, while renowned for his wave theory of light, did not provide a complete or modern explanation of birefringence (double refraction) as we understand it today. However, his work and observations laid some of the crucial groundwork for future understanding of this phenomenon.  

Here’s how Huygens approached birefringence:

Huygens’ Observations and Postulations:

• Discovery by Bartholin: The phenomenon of double refraction in calcite (Iceland spar) was first described in detail by Erasmus Bartholin in 1669. Huygens was aware of Bartholin’s findings and experimented with calcite crystals himself.  
• Two Refracted Rays: Huygens observed that when a ray of unpolarized light enters a calcite crystal at an angle to its optical axis, it splits into two refracted rays:
  • The ordinary ray behaves according to the standard law of refraction (Snell’s Law) and travels at a constant velocity in all directions within the crystal.  
  • The extraordinary ray does not follow Snell’s Law in the same way, and its velocity depends on the direction of propagation within the crystal.  
• Huygens’ Principle and Wavefronts: Huygens explained the propagation of light using his wave theory, where he proposed that every point on a wavefront acts as a source of secondary spherical wavelets. The envelope of these wavelets forms the new wavefront.  
• Explanation Attempt for Birefringence: In his Treatise on Light (published in 1690), Huygens attempted to explain birefringence based on his wave theory. He postulated that within the calcite crystal:
  • There were two different types of wave motion, or two “media” for the propagation of light waves.  
  • One wave propagated with a spherical wavefront, corresponding to the ordinary ray, with a constant velocity in all directions (similar to light in an isotropic medium).
  • The other wave propagated with an ellipsoidal wavefront, corresponding to the extraordinary ray. He reasoned that the velocity of this wave depended on the direction within the crystal, leading to the ellipsoidal shape of the wavefront.  

Limitations of Huygens’ Explanation:

While Huygens’ explanation was a significant step forward in understanding the behavior of light in birefringent materials, it had limitations:

• Nature of the Two Waves: Huygens did not correctly identify the polarization of the two rays. He didn’t understand that the ordinary and extraordinary rays have mutually perpendicular polarizations.
• Longitudinal vs. Transverse Waves: Huygens believed light waves were longitudinal (vibrations parallel to the direction of propagation), similar to sound waves. This model struggled to explain phenomena like polarization, which is a key aspect of birefringence. A transverse wave theory (vibrations perpendicular to the direction of propagation) is necessary to fully account for polarization effects.  
• Interaction with the Crystal Structure: Huygens’ explanation was primarily geometric and kinematic. He didn’t have a detailed understanding of how the anisotropic crystal structure of calcite (where the arrangement of atoms is not the same in all directions) causes the different refractive indices for different polarizations of light.

Later Developments:

It was much later, with the development of a transverse wave theory of light (primarily by Young and Fresnel in the early 19th century) and the understanding of polarization, that a more complete explanation of birefringence emerged. This later understanding incorporated the idea that the anisotropic crystal structure causes light waves with different polarizations to experience different refractive indices and therefore travel at different speeds along different directions within the crystal.  

In conclusion, Christiaan Huygens made a crucial early attempt to explain birefringence using his wave theory of light by proposing two different wavefront shapes (spherical and ellipsoidal) for the two refracted rays. However, his lack of understanding of light’s transverse nature and polarization meant his explanation was incomplete. His work, nevertheless, was foundational in shifting the understanding of light from a purely corpuscular (particle-based) view towards a wave-based one, paving the way for later, more accurate explanations of phenomena like birefringence.

 

Mathematics

Christiaan Huygens: Probability Theory

Christiaan Huygens made a foundational contribution to the development of probability theory by publishing his short treatise, “De ratiociniis in ludo aleae” (On Reasoning in Games of Chance) in 1657. This work, the final chapter in Frans van Schooten’s Latin translation of his mathematical exercises, is considered the first printed work dedicated to the mathematical treatment of probability.  

Here are some key aspects of Huygens’ work on probability theory:

• Concept of Expectation: Huygens introduced and heavily relied on the concept of “expectation” (or “value of a chance”). He defined a player’s expectation in a game of chance as the value of their potential winnings, based on the likelihood of different outcomes. This is a precursor to the modern concept of expected value.  
  • His fundamental principle stated that the value of any chance to win something is precisely the sum for which one could purchase the same chance in a fair game.
• Focus on Games of Chance: His treatise primarily dealt with analyzing probabilities in the context of games of chance, such as dice games and the “problem of points” (how to divide the stakes in an unfinished game).
• Solving the Problem of Points: Huygens provided his own solution to the famous “problem of points,” which Pascal and Fermat had previously discussed in their correspondence. His solution, based on the concept of expectation, aligned with theirs.
• No Explicit Use of “Probability”: Interestingly, Huygens did not explicitly use the word “probability” in his solutions. Instead, he framed his analysis in terms of expectations and the “value” of different chances. To Huygens and his contemporaries, “chance” often implied uncertainty and unpredictability, which seemed at odds with the idea of calculated values.
• Reduction to Equiprobable Cases: Huygens solved problems by reducing them to scenarios with equally likely outcomes. He considered the outcomes of throwing dice, tossing coins, or drawing lots as paradigms for equipossible events. He then broke down more complex problems into these elementary cases.  
• Fundamental Propositions: His treatise laid out several fundamental propositions for calculating expectations in different situations:
  • Proposition I: If one has an equal chance of obtaining amount a or amount b, then the expectation is (a + b) / 2.
  • Proposition II: Extended this to three equally likely amounts.
  • Proposition III (Central Proposition): If there are p equally likely cases for gaining amount a and q equally likely cases for gaining amount b, then the expectation is (pa + qb) / (p + q).
• Influence on Later Probabilists: Huygens’ work, despite its brevity, was highly influential. Jacob Bernoulli, a key figure in the further development of probability theory, included an annotated version of Huygens’ treatise as the first part of his famous “Ars Conjectandi” (The Art of Conjecturing) published posthumously in 1713. Huygens’ focus on expected values provided a crucial foundation for later developments in the field.  

In summary, while Christiaan Huygens didn’t use the term “probability” extensively, his 1657 treatise on games of chance was a groundbreaking work that introduced the concept of expectation and provided the first systematic mathematical analysis of probabilistic scenarios. His methods and principles laid the essential groundwork for the subsequent development of probability theory by later mathematicians.

 

Christiaan Huygens: Work on Curves

Here’s an image related to Christiaan Huygens’ work on curves:

Christiaan Huygens made significant contributions to the understanding and theory of curves, particularly in the context of his work on mechanics and optics. His investigations went beyond simply studying known curves and delved into their properties and relationships. Here are some key areas of his work on curves:  

1. The Cycloid and the Tautochrone Problem:

• The Cycloid: Huygens extensively studied the cycloid, the curve traced by a point on the rim of a rolling circle. This curve became central to his work on pendulum clocks.  
• Tautochrone Curve: He is most famous for identifying the cycloid as the tautochrone curve. This means that a pendulum swinging along a cycloidal arc, even with different amplitudes, will have the same period. This was crucial for developing more accurate pendulum clocks, as a simple circular pendulum’s period depends on its swing’s amplitude.  
• In his groundbreaking work, Horologium Oscillatorium sive de motu pendulorum (The Pendulum Clock and the Motion of Pendulums) published in 1673, Huygens provided a geometric proof that the cycloid possesses this unique property.  
• He even attempted to build pendulum clocks with cycloidal cheeks to force the pendulum bob to move along a cycloidal path, although practical limitations like friction hindered its widespread adoption.  

2. Evolutes and Involutes of Curves:

• Huygens developed the theory of evolutes and involutes of curves.  
• Evolute: The evolute of a curve is the locus of its centers of curvature. It can also be defined as the envelope of the normals to the curve.
• Involute: An involute of a curve is the path traced by the end of a taut string as it is unwound from the curve. A curve can have infinitely many involutes, depending on the starting point of the unwinding.  
• In Horologium Oscillatorium, Huygens defined evolutes and involutes and derived some of their fundamental properties.  
• He notably found that the evolute of the cycloid is another cycloid of the same shape and size, just translated. This property was key to his attempts to create an isochronous pendulum. He reasoned that the bob would be forced to move along a cycloidal arc by suspending a pendulum bob from a string that wraps around cycloidal cheeks (the evolute of the desired path).
• He also determined the evolutes of other curves, such as the parabola.

3. Applications to Mechanics:

• Huygens’s work on curves was deeply intertwined with his investigations into mechanics, particularly the motion of falling bodies and pendulums.
• His understanding of curve properties, such as the cycloid’s tautochrone property, directly led to his advancements in horology.
• He also studied the descent of bodies along curves in a vacuum, as described in Horologium Oscillatorium.  

4. Relationship with Optics:

• While his most famous work on optics, the wave theory of light, doesn’t directly involve the geometric study of curves in the same way as his mechanics research, his understanding of geometric principles was fundamental to his scientific approach.
• He also explored caustics, which are related to evolutes and are formed by the envelope of light rays reflected or refracted by a curve or surface.

In summary, Christiaan Huygens made significant and original contributions to the theory of curves, most notably through his detailed analysis of the cycloid and his development of the concepts of evolutes and involutes. His work was driven by his practical concerns, such as improving the accuracy of clocks, and his theoretical investigations in mechanics, demonstrating the power of geometric understanding in solving physical problems. His Horologium Oscillatorium stands as a testament to his deep insights into the mathematical properties of curves and their profound implications for the physical world.

 

Galileo Galilei, Johannes Kepler, and Christiaan Huygens: Similarities

While Galileo Galilei, Johannes Kepler, and Christiaan Huygens each had unique approaches and made distinct, groundbreaking contributions, they shared several important similarities that mark them as pivotal figures of the 17th-century Scientific Revolution:

1. Pioneers of the Scientific Revolution: All three were central figures who actively participated in and drove the profound shift away from ancient and medieval scientific paradigms towards a new understanding of the natural world based on observation, experimentation, and mathematical reasoning.
2. Emphasis on Mathematics: Each recognized the power of mathematics as a fundamental tool for describing and understanding the physical universe. Kepler’s laws are explicitly mathematical, Galileo applied mathematics to the study of motion, and Huygens used sophisticated geometry and early calculus concepts in his work.  
3. Revolutionary Contributions to Astronomy: All made foundational and transformative contributions to astronomy. They were instrumental in observing, describing, and providing a theoretical framework for the workings of the solar system.
4. Critical Role of the Telescope: Their astronomical work was deeply intertwined with the telescope:
   • Galileo was a pioneering user who made groundbreaking discoveries with it.  
   • Kepler not only used it to confirm observations but also made significant theoretical contributions to its optics and designed an improved version (the Keplerian telescope).  
   • Huygens significantly improved telescope construction (lenses, eyepieces) and used these enhanced instruments for new discoveries.  
5. Challenging Ancient Authority: Their collective work, particularly in astronomy, directly challenged and helped overturn the long-dominant Aristotelian and Ptolemaic geocentric worldview, paving the way for the widespread acceptance and refinement of the heliocentric model.  
6. Contributions to Optics: Beyond just using telescopes, all three made contributions to the science of optics. Kepler wrote extensively on how lenses work, Galileo’s work inherently involved practical optics, and Huygens developed his influential wave theory of light.
7. Broad Scientific Inquiry: While renowned for astronomy, their scientific interests were broad. Galileo made fundamental contributions to physics (motion), Kepler to mathematics and optics, and Huygens to mechanics (pendulum clock, centrifugal force), optics, and probability theory.
8. Dedication to Empirical Evidence & Observation: While Kepler also had strong philosophical and even mystical motivations, his ultimate reliance on Tycho Brahe’s precise observational data was crucial. Galileo famously championed empirical observation and experimentation. Huygens was also a skilled experimentalist and observer.  
9. Dissemination of Knowledge: All three published influential works communicated their findings and theories, contributing to the spread of new scientific ideas across Europe, despite facing challenges (like Galileo’s conflict with the Church).
10. Enduring Legacy: Their discoveries and methodologies laid essential groundwork for subsequent scientists, most notably Isaac Newton, whose work built upon their insights into motion, optics, and celestial mechanics.  

These shared characteristics underscore their collective importance in shaping the course of modern science.

 

Galileo Galilei, Johannes Kepler, and Christiaan Huygens Differences

While Galileo Galilei, Johannes Kepler, and Christiaan Huygens were all towering figures of the 17th-century Scientific Revolution and shared common goals in advancing understanding of the natural world, they had distinct primary focuses, methodologies, landmark contributions, and contexts:

1. Galileo Galilei (Italian, 1564–1642):  
   • Primary Focus: Observational Astronomy & Experimental Physics. Galileo’s greatest impact came from being arguably the first to use the telescope for astronomical observations systematically and championing the empirical method.
   • Key Method: Direct observation with his improved telescopes, experimentation (e.g., with falling bodies and pendulums), and persuasive argumentation, often through widely accessible Italian dialogues.
   • Landmark Astronomical Contribution: His telescopic discoveries (Jupiter’s moons, Moon’s craters, phases of Venus, sunspots, Milky Way’s stars) provided powerful visual evidence challenging the geocentric Ptolemaic system and supporting Copernican heliocentrism.  
   • Relationship with Theory: He was primarily an observer and experimentalist who used his findings to support existing theories (Copernicanism) or develop new empirical laws (e.g., for falling bodies), rather than devising grand mathematical cosmological systems himself.  
   • Major Conflict: His advocacy for heliocentrism as a physical reality led to direct conflict with the Catholic Church, culminating in his trial and house arrest.  
   • Key Works: Sidereus Nuncius (1610), Dialogue Concerning the Two Chief World Systems (1632), Discourses and Mathematical Demonstrations Relating to Two New Sciences (1638).  
2. Johannes Kepler (German, 1571–1630):  
   • Primary Focus: Mathematical Astronomy & Celestial Mechanics. Kepler’s main goal was to discover the mathematical laws governing planetary motion.
   • Key Method: Rigorous mathematical analysis of the most precise astronomical observations available at the time (primarily those of Tycho Brahe). He was driven by a belief in a divinely ordered, harmonious universe describable by geometry.
   • Landmark Astronomical Contribution: His Three Laws of Planetary Motion, which described orbits as elliptical (not circular), provided the precise mathematical foundation for the heliocentric model and revolutionized astronomy.
   • Relationship with Theory: He was a profound theorist, moving beyond Copernicus by abandoning circular orbits and seeking physical explanations (though not yet gravity) for planetary movements. He also made significant contributions to optics, explaining how telescopes work and designing the “Keplerian telescope.”  
   • Major Conflict: Faced religious persecution as a Protestant and significant personal hardships, but his primary struggles were often intellectual and financial in pursuit of his complex calculations.  
   • Key Works: Astronomia Nova (1609), Harmonices Mundi (1619), Epitome Astronomiae Copernicanae (1618-1621), Rudolphine Tables (1627).
3. Christiaan Huygens (Dutch, 1629–1695):  
   • Primary Focus: Physics (Optics & Mechanics), Horology, and Advanced Telescopic Observation. Huygens was a brilliant physicist, instrumentalist, and astronomer.  
   • Key Method: Mathematical analysis, sophisticated experimentation, and the design and construction of advanced scientific instruments.
   • Landmark Astronomical Contribution: His discovery of Saturn’s largest moon, Titan, and his correct interpretation of Saturn’s rings as a thin, flat system not touching the planet, made possible by his superior self-made telescopes.
   • Relationship with Theory: He developed the wave theory of light, a major alternative to Newton’s corpuscular theory, and made foundational contributions to mechanics (e.g., centrifugal force, elastic collisions). His invention of the pendulum clock provided an unprecedented tool for accurate time measurement, vital for astronomical observations.
   • Major Conflict: Engaged in scientific debates (e.g., with Newton over the nature of light and gravity), but did not face the kind of institutional conflict Galileo did.
   • Key Works: Systema Saturnium (1659), Horologium Oscillatorium (1673), Traité de la Lumière (1690).

In summary of key differences:

• Approach to Astronomy:
  • Galileo: Primarily observational, providing groundbreaking empirical evidence.  
  • Kepler: Primarily theoretical and mathematical, deducing fundamental laws from data.
  • Huygens: A blend of advanced observation (with superior instruments he helped design), theoretical physics (optics, mechanics), and invention.
• Primary Impact on Heliocentrism:
  • Galileo: Popularized it and provided strong observational support that challenged the old model.  
  • Kepler: Provided the accurate mathematical description and laws for the heliocentric system.  
  • Huygens: His discoveries further detailed the solar system within a broadly accepted (by then, in scientific circles) heliocentric view and provided physical theories (like wave optics) relevant to astronomical phenomena.  
• Relationship with Technology:
  • Galileo: Improved and masterfully utilized the early telescope.  
  • Kepler: Theorized about telescope optics and designed an improved type.  
  • Huygens: Master lens grinder, significantly advanced telescope design (Huygenian eyepiece), and invented the pendulum clock, crucial for precise astronomical work.  

Their individual strengths and focuses complemented each other, collectively driving the astronomical revolution of the 17th century.

 

Galileo Galilei, Johannes Kepler, and Christiaan Huygens Compared Table

Okay, here’s a comparative table for Galileo Galilei, Johannes Kepler, and Christiaan Huygens, focusing on their roles in the 17th-century astronomical revolution driven by the telescope and their other key scientific contributions.

Feature	Galileo Galilei (Italian, 1564–1642)	Johannes Kepler (German, 1571–1630)	Christiaan Huygens (Dutch, 1629–1695)
Primary Role in the Telescopic Revolution	Pioneering observational astronomer; popularized the telescope for celestial study; provided key evidence for Copernicanism.	Theoretical astronomer providing mathematical laws for heliocentrism; advanced optical theory for telescopes.	Advanced telescope design and observational capabilities; made new significant discoveries with improved instruments.
Key Telescopic Discoveries	Moons of Jupiter, Moon’s craters/mountains, phases of Venus, Milky Way’s stars, sunspots.	Confirmed Galileo’s discoveries (e.g., Jupiter’s moons).	Saturn’s moon Titan, the true nature of Saturn’s rings, and resolved features in the Orion Nebula.
Key Theoretical Contributions (Astronomy/Optics)	Qualitative arguments for heliocentrism based on observation.	Three Laws of Planetary Motion; theories on light refraction and vision (Astronomiae Pars Optica).	Wave theory of light (Traité de la Lumière); analysis of optics for telescopes.
Key Invention/Instrumental Design	Significantly improved early refracting telescopes (higher magnification).	Designed the “Keplerian Telescope” (using two convex lenses, wider field of view).	Invented the Pendulum Clock (vital for precise timing); developed the Huygenian eyepiece for telescopes.
Other Major Scientific Contributions	Laws of falling bodies, principle of inertia, kinematics (in Two New Sciences).	Work on logarithms, infinitesimal calculus precursors, geometric harmonies.	Work on centrifugal force, laws of elastic collision, probability theory, and mechanics (Horologium Oscillatorium).
Major Work(s)	Sidereus Nuncius (1610), Dialogue Concerning the Two Chief World Systems (1632), Two New Sciences (1638).	Astronomia Nova (1609), Dioptrice (1611), Harmonices Mundi (1619), Rudolphine Tables (1627).	Systema Saturnium (1659), Horologium Oscillatorium (1673), Traité de la Lumière (1690).
Impact on Prevailing Cosmology	Directly challenged Aristotelian/Ptolemaic geocentrism with strong observational evidence.	Provided the precise mathematical laws that described a heliocentric system, replacing circular orbits with ellipses.	His discoveries (Saturn’s rings, Titan) expanded knowledge of the solar system and complexity beyond Earth.
Primary Method	Observation and experimentation.	Mathematical analysis of observational data (primarily Tycho Brahe’s) and theoretical modeling.	Experimentation, mathematical analysis, instrument design, and construction.

Export to Sheets

These three figures, through their distinct yet interconnected work with the telescope and their broader scientific inquiries, were instrumental in transforming our understanding of the universe during the 17th century.